题目内容
已知数列 的前
的前 项和
项和 ,函数
,函数 对
对 有
有 ,数列
,数列 满足
满足
 .
.
(1)分别求数列 、
、 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
,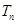 是数列
是数列 的前
的前 项和,若存在正实数
项和,若存在正实数 ,使不等式
,使不等式 对于一切的
对于一切的 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 的前
的前 项和
项和 ,函数
,函数 对
对 有
有 ,数列
,数列 满足
满足
 .
.(1)分别求数列
 、
、 的通项公式;
的通项公式;(2)若数列
 满足
满足 ,
,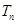 是数列
是数列 的前
的前 项和,若存在正实数
项和,若存在正实数 ,使不等式
,使不等式 对于一切的
对于一切的 恒成立,求
恒成立,求 的取值范围.
的取值范围.(1)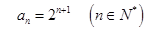 (2)
(2)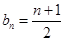
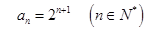 (2)
(2)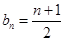
试题分析:(1)由数列
 的前
的前 项和
项和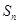 求
求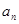 ,分两种情况进行,
,分两种情况进行, 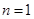 时
时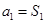 和
和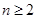 时,
时, 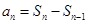 .数列
.数列 利用
利用 可求得.
可求得.(2)由(1)得
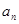 ,
, 利用
利用 得出
得出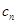 关系式,利用错位相减法得出
关系式,利用错位相减法得出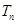 ,再利用参数分离法得出k的范围.
,再利用参数分离法得出k的范围.试题解析:(1)
 1分
1分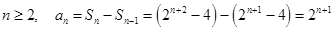
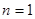 时满足上式,故
时满足上式,故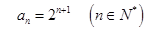 3分
3分∵
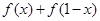 =1∴
=1∴ 4分
4分∵

 ①
①∴

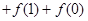 ②
②∴①+②,得
 6分
6分(2)

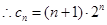 7分
7分 ①
①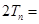
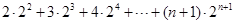 ②
②①-②得
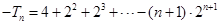 8分
8分即
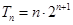 10分
10分要使得不等式
 恒成立,
恒成立,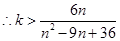 对于一切的
对于一切的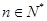 恒成立,
恒成立,即
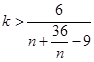 11分
11分令
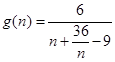 ,则
,则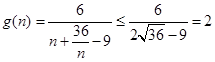
当且仅当
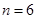 时等号成立,故
时等号成立,故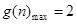 13分
13分所以
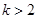 为所求. 14分
为所求. 14分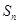 求
求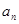 ,错位相减法,参数分离.
,错位相减法,参数分离.
练习册系列答案
相关题目
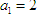 ,点
,点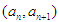 在函数
在函数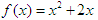 的图象上,其中
的图象上,其中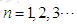
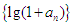 是等比数列,并求数列
是等比数列,并求数列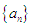 的通项公式;
的通项公式;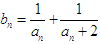 ,求数列
,求数列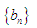 的前
的前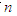 项和
项和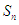 .
. (i,j∈N*).例如
(i,j∈N*).例如 ,若
,若
 ,则其前n项和Sn=________.
,则其前n项和Sn=________. 中,若
中,若 ,
, ,则
,则 .
.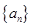 的前
的前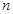 项和为
项和为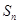 ,且
,且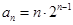 ,则
,则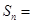 ______________.
______________.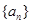 ,
,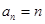 ,则数列
,则数列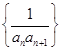 的前10项和为( )
的前10项和为( )



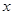 ,用
,用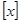 表示不超过
表示不超过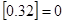 ,
,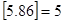 ,若
,若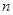 为正整数,
为正整数,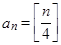 ,
,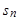 为数列
为数列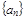 的前
的前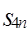 __________________________;
__________________________; 的前
的前 项和为
项和为 ,若
,若 (
( ),则
),则 .
.