题目内容
若f(x)=x2-x+a,f(-m)<0,则f(m+1)的值是( )
| A．正数 | B．负数 |
| C．非负数 | D．不能确定正负 |
B
解析
练习册系列答案
相关题目
已知
是定义在
上的奇函数，满足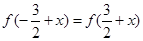
,当
时,
，则函数在区间
上的零点个数是（ ）
| A．3 | B．5 | C．7 | D．9 |
给定函数①y=
,②y=
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
| A．①② | B．②③ |
| C．③④ | D．①④ |
若在曲线f(x,y)=0上存在两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”.下列方程:①x2-y2=1;②y=x2-|x|;③y=3sinx+4cosx;④|x|+1=
对应的曲线中存在“自公切线”的有( )
| A．①② | B．②③ |
| C．①④ | D．③④ |
定义在R上的函数y=f(x+1)的图象如图所示,它在定义域上是减函数,给出如下命题:①f(0)=1;②f(-1)=1;③若x>0,则f(x)<0;④若x<0,则f(x)>0,其中正确的是( )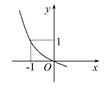
| A．②③ | B．①④ | C．②④ | D．①③ |
“a≤0”是“函数f(x)＝|(ax－1)x|在区间(0，＋∞)内单调递增”的( )
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
对于函数f(x)=acosx+bx2+c,其中a,b,c∈R,适当地选取a,b,c的一组值计算f(1)和f(-1),所得出的正确结果只可能是( )
| A．4和6 | B．3和-3 |
| C．2和4 | D．1和1 |
已知函数f(x)为奇函数，且当x>0时， f(x) ＝x2＋
，则f(－1)＝( )
| A．－2 | B．0 |
| C．1 | D．2 |