题目内容
2.已知二次函数f(x)=x2+2ax+a-1,a为常数.(1)设函数F(x)=f(x)-ax+1,若F(x)有唯一零点,求a的值.
(2)求函数f(x)在[-1,2]上的最小值g(a)的解析式;
(3)在(2)的条件下,是否存在最小的整数m,使得g(a)-m≤0对于任意的a∈R均成立,若存在,求出m的值;若不存在,请说明理由.
分析 (1)F(x)=f(x)-ax+1=x2+ax+a=0,利用判别式=0,即可求a的值.
(2)由函数的解析式可得函数开口方向及对称轴,分类讨论给定区间与对称轴的关系,分析函数的单调性后,可得最值;
(3)若g(a)-m≤0恒成立,则m不小于g(a)的最大值,分析函数g(a)的单调性求其最值可得答案.
解答 解:(1)F(x)=f(x)-ax+1=x2+ax+a=0,
∴△=a2-4a=0,
∴a=0或4;
(1)对称轴x=-a
①当-a≤-1⇒a≥1时,
f(x)在[-1,2]上是增函数,x=-1时有最小值f(-1)=-a;
②当-a≥2⇒a≤-2时,
f(x)在[-1,2]上是减函数,x=2时有最小值f(2)=3a+3;
③当-1<-a<2⇒-2<a<1时,
f(x)在[-1,2]上是不单调,x=-a时有最小值f(-a)=-a2-a-1;
∴g(a)=$\left\{\begin{array}{l}{-a,a≥1}\\{-{a}^{2}-a-1,-2<a<1}\\{3a+3,a≤-2}\end{array}\right.$;
(2)存在,
由题知g(a)在(-∞,-$\frac{1}{2}$]是增函数,在[-$\frac{1}{2}$,+∞)是减函数
∴a=-$\frac{1}{2}$时,g(a)max=-$\frac{3}{4}$,
∵g(a)-m≤0恒成立
∴g(a)max≤m,
∴m≥-$\frac{3}{4}$,
∵m为整数,
∴m的最小值为0.
点评 本题考查的知识点是函数的恒成立问题,函数解析式的求法,考查分类讨论、转化思想,属于中档题.

练习册系列答案
相关题目
12.已知全集U={1,2,4,6,8,10},集合A={2,8},B={2,4,10},则∁U(A∩B)=( )
| A. | {2,4,8,10} | B. | {1,6} | C. | {1,4,6,8,10} | D. | {2,6} |
17.已知函数f(x)满足:当x≥3时.f(x)=($\frac{1}{2}$)x;当x<3时,f(x)=f(x+1),则f($\frac{5}{2}$)的值为( )
| A. | $\frac{\sqrt{2}}{16}$ | B. | $\frac{\sqrt{3}}{16}$ | C. | $\frac{\sqrt{2}}{32}$ | D. | $\frac{\sqrt{3}}{32}$ |
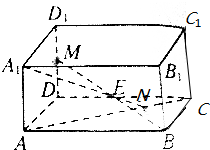 已知长方体ABCD-A1B1C1D1中,M为DD1的中点,N在AC上,且AN:NC=2:1,E为BM的中点.求证:A1,E,N三点共线.
已知长方体ABCD-A1B1C1D1中,M为DD1的中点,N在AC上,且AN:NC=2:1,E为BM的中点.求证:A1,E,N三点共线.