题目内容
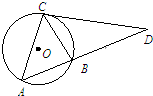 如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,且CD=2
如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,且CD=2| 7 |
3
| ||
| 2 |
3
| ||
| 2 |
分析:由已知CD是过点C圆的切线,根据切割线定理及已知中CD=2
,AB=BC=3,易求出BD的长,进而求出AD的长,由弦切角定理可得:∠DCB=∠A,又由∠D是△DCB与△DAC的公共角,我们易得△DCB∽△DAC根据三角形相似对应边成比例,我们即可求出AC的长.
| 7 |
解答:解:∵CD是过点C圆的切线
DBA为圆的割线
由切割线定理得:
CD2=DB•DA
由CD=2
,AB=BC=3
解得BD=4
∴DA=7
由弦切角定理可得:∠DCB=∠A,又由∠D=∠D
∴△DCB∽△DAC
∴BC•DA=AC•CD
由BC=3,DA=7,CD=2
,得
AC=
故答案为:
DBA为圆的割线
由切割线定理得:
CD2=DB•DA
由CD=2
| 7 |
解得BD=4
∴DA=7
由弦切角定理可得:∠DCB=∠A,又由∠D=∠D
∴△DCB∽△DAC
∴BC•DA=AC•CD
由BC=3,DA=7,CD=2
| 7 |
AC=
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |
点评:本题考查的知识点是切割线定理,弦切角定理,三角形相似的判定与性质,要求线段的长,我们一般要要先分析已知线段与未知线段的位置关系,再选择恰当的定理或性质进行解答.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2
如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2 如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P. 如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2
如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2 (2012•通州区一模)如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,AB=BC=3,CD=2
(2012•通州区一模)如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,AB=BC=3,CD=2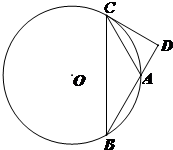 (2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若
(2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若