题目内容

14．如果a，b，c∈R，那么“b2＞4ac”是“方程ax2+bx+c=0有两个不等实根”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 根据充分条件和必要条件的定义进行判断即可．

解答 解：若方程ax2+bx+c有两个不等实根，
则判别式△=b2-4ac＞0，
则当b=1，a=0，满足“b2＞4ac”，但方程ax2+bx+c=0等价为x+c=0，此时方程有两个不等实根不成立，
即“b2＞4ac”是“方程ax2+bx+c=0有两个不等实根”的必要不充分条件，
故选：B

点评 本题主要考查充分条件和必要条件的判断，根据一元二次方程根与判别式△的关系是解决本题的关键．

练习册系列答案
相关题目
4．已知函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜2π）的图象在y轴上的截距为1，且它在右侧的第一个最大值点为（2，$\sqrt{2}$）．求函数的解析式．
5．已知函数f（x）=x2-4ax+2a+6．
（1）若函数f（x）有零点，求实数a的范围；
（2）在（1）的条件下，求g（a）=2-a•|a+3|的值域．
2．设定义在R上的函数f（x）、g（x）满足$\frac{f（x）}{g（x）}$=ax，且f′（x）g（x）＞f（x）g′（x），$\frac{f（1）}{g（1）}$+$\frac{f（-1）}{g（-1）}$=$\frac{5}{2}$，则有穷数{$\frac{f（n）}{g（n）}$+2n-1}（n∈N*）的前8项和为（　　）
A．574B．576C．1088D．1090
9．设函数f（x）=2x3+x-5，求f（-2），f（4），f（b），f（b+h）．
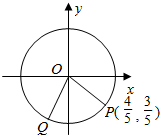19．已知角α、β的终边分别与⊙O：x2+y2=1交于点P（$\frac{4}{5}$，-$\frac{3}{5}$）、且OP⊥OQ，则sinα=-$\frac{3}{5}$，tanβ=$\frac{4}{3}$．
6．已知函数f（x）=loga$\frac{1-mx}{x-1}$（a＞0，且a≠1，m≠1）是奇函数．
（1）求实数m的值；
（2）探究函数f（x）在（1，+∞）上的单调性；
（3）若a=2，试求函数f（x）在[3，5]上的值域．
3．已知函数y=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x，求函数的振幅、角速度、初相位．
6．写出下列命题的否定，并判断其真假
（1）p：如果a，b，c成等差数列，则2b=a+c；
（2）q：等圆的面积相等，周长相等；
（3）r：任何三角形的外角都至少有两个钝角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网