题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,若不等式
时,若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)
;(II)![]()
【解析】
试题分析:(I)求出![]() 时,
时,![]() ,根据直线方程的点斜式可得切线方程;(II)当
,根据直线方程的点斜式可得切线方程;(II)当![]() 时,若不等式
时,若不等式![]() 恒成立等价于
恒成立等价于![]() ,通过讨论
,通过讨论![]() 的范围,得到其在
的范围,得到其在![]() 上的单调性,分别求出求出最小值,得到
上的单调性,分别求出求出最小值,得到![]() 的范围,最后取并集即得实数
的范围,最后取并集即得实数![]() 的取值范围.
的取值范围.
试题解析:(I)当![]() 时,
时,![]() ,
,
即曲线![]() 在
在![]() 处的切线的斜率为
处的切线的斜率为![]() ,又
,又![]() ,
,
所以所求切线方程为![]() .
.
(II)当![]() 时,若不等式
时,若不等式![]() 恒成立
恒成立![]()
易知![]()
若![]() ,则
,则![]() 恒成立,
恒成立,![]() 在R上单调递增;
在R上单调递增;
又![]() ,所以当
,所以当![]() 时,
时,![]() ,符合题意.
,符合题意.
若![]() ,由
,由![]() ,解得
,解得![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以![]() 时,函数
时,函数![]() 取得最小值.
取得最小值.
则当![]() ,即
,即![]() 时,则当
时,则当![]() 时,
时,![]() ,符合题意.
,符合题意.
当![]() ,即
,即![]() 时,则当
时,则当![]() 时,
时,![]() 单调递增,
单调递增,![]() ,不符合题意.
,不符合题意.
综上,实数![]() 的取值范围是
的取值范围是![]() (没有综上扣一分)
(没有综上扣一分)

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
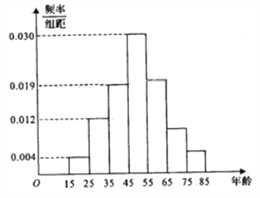
浙江之星课时优化作业系列答案【题目】2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策,为了了解适龄民众对放开生育二胎政策的态度,某市进行了一次民意调查,参与调查的100位市民中,年龄分布情况如下图所示,并得到适龄民众对放开生育二胎政策的态度数据如下表:
生二胎 | 不生二胎 | 合计 | |
25~35岁 | 10 | ||
35~50岁 | 30 | ||
合计 | 100 |
(1)填写上面的![]() 列联表;
列联表;
(2)根据调查数据,有多少的把握认为“生二胎与年龄有关”,说明理由;
(3)调查对象中决定生二胎的民众有六人分别来自三个不同的家庭且为父子,各自家庭都有一个约定:父亲先生二胎,然后儿子生二胎,则这三个家庭“二胎出生的日期的先后顺序”有多少种?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
(参考公式:![]() ,其中
,其中![]() )
)
【题目】衡州市英才中学贯彻党的教育方针,促进学生全面发展,积极组织开展了丰富多样的社团活动,根据调查,英才中学在传统民族文化的继承方面开设了“泥塑”、“剪纸”、“曲艺”三个社团,三个社团参加的人数如下表所示:
社团 | 泥塑 | 剪纸 | 曲艺 |
人数 | 320 | 240 | 200 |
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为![]() 的样本,已知从“剪纸”社团抽取的同学比从“泥塑”社团抽取的同学少2人。
的样本,已知从“剪纸”社团抽取的同学比从“泥塑”社团抽取的同学少2人。
(1)求三个社团分别抽取了多少同学;
(2)若从“剪纸”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“剪纸”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.