ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥“ϊΝœ≥ß…ζ≤ζ![]() ΝΫ÷÷“ϊΝœΘ°…ζ≤ζ1ΆΑ
ΝΫ÷÷“ϊΝœΘ°…ζ≤ζ1ΆΑ![]() “ϊΝœΘ§–ηΗΟΧΊ≤ζ‘≠Νœ100ΙΪΫοΘ§–η ±Φδ3–Γ ±ΘΜ…ζ≤ζ1ΆΑ
“ϊΝœΘ§–ηΗΟΧΊ≤ζ‘≠Νœ100ΙΪΫοΘ§–η ±Φδ3–Γ ±ΘΜ…ζ≤ζ1ΆΑ![]() “ϊΝœ–ηΗΟΧΊ≤ζ‘≠Νœ100ΙΪΫοΘ§–η ±Φδ1–Γ ±Θ§ΟΩΧλ
“ϊΝœ–ηΗΟΧΊ≤ζ‘≠Νœ100ΙΪΫοΘ§–η ±Φδ1–Γ ±Θ§ΟΩΧλ![]() “ϊΝœΒΡ≤ζΝΩ≤Μ≥§Ιΐ
“ϊΝœΒΡ≤ζΝΩ≤Μ≥§Ιΐ![]() “ϊΝœ≤ζΝΩΒΡ2±ΕΘ§ΟΩΧλ…ζ≤ζΝΫ÷÷“ϊΝœΥυ–ηΗΟΧΊ≤ζ‘≠ΝœΒΡΉήΝΩ÷ΝΕύ750ΙΪΫοΘ§ΟΩΧλ…ζ≤ζ
“ϊΝœ≤ζΝΩΒΡ2±ΕΘ§ΟΩΧλ…ζ≤ζΝΫ÷÷“ϊΝœΥυ–ηΗΟΧΊ≤ζ‘≠ΝœΒΡΉήΝΩ÷ΝΕύ750ΙΪΫοΘ§ΟΩΧλ…ζ≤ζ![]() “ϊΝœΒΡ ±Φδ≤ΜΒΆ”Ύ…ζ≤ζ
“ϊΝœΒΡ ±Φδ≤ΜΒΆ”Ύ…ζ≤ζ![]() “ϊΝœΒΡ ±ΦδΘ§ΟΩΆΑ
“ϊΝœΒΡ ±ΦδΘ§ΟΩΆΑ![]() “ϊΝœΒΡάϊ»σ «ΟΩΆΑ
“ϊΝœΒΡάϊ»σ «ΟΩΆΑ![]() “ϊΝœάϊ»σΒΡ1.5±ΕΘ§»τΗΟ“ϊΝœ≥ßΟΩΧλ…ζ≤ζ
“ϊΝœάϊ»σΒΡ1.5±ΕΘ§»τΗΟ“ϊΝœ≥ßΟΩΧλ…ζ≤ζ![]() “ϊΝœ
“ϊΝœ![]() ΆΑΘ§
ΆΑΘ§![]() “ϊΝœ
“ϊΝœ![]() ΆΑ ±Θ®
ΆΑ ±Θ®![]() Θ©άϊ»σΉν¥σΘ§‘ρ
Θ©άϊ»σΉν¥σΘ§‘ρ![]() _____Θ°
_____Θ°
ΓΨ¥πΑΗΓΩ7
ΓΨΫβΈωΓΩ
…ηΟΩΧλ![]() ΝΫ÷÷“ϊΝœΒΡ…ζ≤ζ ΐΝΩΖ÷±π «
ΝΫ÷÷“ϊΝœΒΡ…ζ≤ζ ΐΝΩΖ÷±π «![]() ΆΑΘ§
ΆΑΘ§![]() ΆΑΘ§”…Χβ“βΩ…ΒΟ‘Φ χΧθΦΰΈΣΘ§
ΆΑΘ§”…Χβ“βΩ…ΒΟ‘Φ χΧθΦΰΈΣΘ§
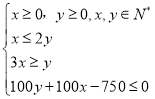 Θ§Ής≥ωΩ…––”ρΘ§ΡΩ±ξΚ· ΐΈΣ
Θ§Ής≥ωΩ…––”ρΘ§ΡΩ±ξΚ· ΐΈΣ![]() Θ§ΤΫ“Τ÷±œΏ
Θ§ΤΫ“Τ÷±œΏ![]() Θ§Ω…ΒΟΒ±
Θ§Ω…ΒΟΒ±![]() Ιΐ
Ιΐ![]() ±Θ§
±Θ§![]() »ΓΉν¥σΘ§”…¥ΥΩ…ΒΟ
»ΓΉν¥σΘ§”…¥ΥΩ…ΒΟ![]() ΒΡ÷ΒΘ§ΫχΕχΩ…«σ≥ω
ΒΡ÷ΒΘ§ΫχΕχΩ…«σ≥ω![]() .
.
…ηΟΩΧλ![]() ΝΫ÷÷“ϊΝœΒΡ…ζ≤ζ ΐΝΩΖ÷±π «
ΝΫ÷÷“ϊΝœΒΡ…ζ≤ζ ΐΝΩΖ÷±π «![]() ΆΑΘ§
ΆΑΘ§![]() ΆΑΘ§‘ρ”–
ΆΑΘ§‘ρ”–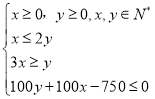 Θ§
Θ§
»τΚω¬‘![]() Θ§‘ρΤδ±μ ΨΒΡΩ…––”ρ»γΆΦ÷–“θ”Α≤ΩΖ÷Υυ ΨΘ§…ηάϊ»σΈΣ
Θ§‘ρΤδ±μ ΨΒΡΩ…––”ρ»γΆΦ÷–“θ”Α≤ΩΖ÷Υυ ΨΘ§…ηάϊ»σΈΣ![]() Θ§
Θ§
‘ρ![]() Θ§¥”Εχ
Θ§¥”Εχ![]() Θ§
Θ§![]() ±μ Ψ÷±œΏ‘Ύ
±μ Ψ÷±œΏ‘Ύ![]() ÷α…œΒΡΫΊΨύΘ§Μ≠≥ω
÷α…œΒΡΫΊΨύΘ§Μ≠≥ω![]() Θ§
Θ§
”…![]() Θ§
Θ§![]() Ω…ΒΟ
Ω…ΒΟ![]() ,
,
“ρΈΣ![]() Θ§‘ρΒ±
Θ§‘ρΒ±![]() Ιΐ
Ιΐ![]() ±Θ§
±Θ§![]() »ΓΉν¥σΘ§¥Υ ±
»ΓΉν¥σΘ§¥Υ ±![]()
Φ¥Β±![]() ±Θ§άϊ»σΉν¥σΘ§¥Υ ±
±Θ§άϊ»σΉν¥σΘ§¥Υ ±![]() .
.
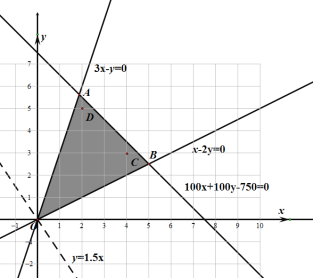
Ι ¥πΑΗΈΣ:7Θ°

ΓΨΧβΡΩΓΩΡ≥ΉήΙΪΥΨ‘ΎAΘ§BΝΫΒΊΖ÷±π”–ΦΉΓΔ““ΝΫΗωœ¬ τΙΪΥΨΆ§÷÷–¬Ρή‘¥≤ζΤΖΘ®’βΝΫΗωΙΪΥΨΟΩΧλΕΦΙΧΕ®…ζ≤ζ50Φΰ≤ζΤΖΘ©Θ§Υυ…ζ≤ζΒΡ≤ζΤΖΨυ‘Ύ±ΨΒΊœζ έ.≤ζΤΖΫχ»Υ –≥Γ÷°«Α–η“ΣΕ‘≤ζΤΖΫχ–––‘ΡήΦλ≤βΘ§ΒΟΖ÷ΒΆ”Ύ80Ζ÷ΒΡΕ®ΈΣ¥ΈΤΖΘ§–η“ΣΖΒ≥ß‘ΌΦ”ΙΛΘΜΒΟΖ÷≤ΜΒΆ”Ύ80Ζ÷ΒΡΕ®ΈΣ’ΐΤΖΘ§Ω…“‘Ϋχ»Υ –≥Γ.Φλ≤β‘±Ά≥ΦΤΝΥΦΉΓΔ““ΝΫΗωœ¬ τΙΪΥΨ100ΧλΒΡ…ζ≤ζ«ιΩωΦΑΟΩΦΰ≤ζΤΖ”·άϊΩςΥπ«ιΩωΘ§ ΐΨί»γ±μΥυ ΨΘΚ
±μ1
ΦΉΙΪΥΨ | ΒΟΖ÷ | [50Θ§60Θ© | [60Θ§70Θ© | [70Θ§80Θ© | [80Θ§90Θ© | [90Θ§100] |
Φΰ ΐ | 10 | 10 | 40 | 40 | 50 | |
Χλ ΐ | 10 | 10 | 10 | 10 | 80 |
±μ2
ΦΉΙΪΥΨ | ΒΟΖ÷ | [50Θ§60Θ© | [60Θ§70Θ© | [70Θ§80Θ© | [80Θ§90Θ© | [90Θ§100] |
Φΰ ΐ | 10 | 5 | 40 | 45 | 50 | |
Χλ ΐ | 20 | 10 | 20 | 10 | 70 |
±μ3
ΟΩΦΰ’ΐΤΖ | ΟΩΦΰ¥ΈΤΖ | |
ΦΉΙΪΥΨ | ”·2Άρ‘Σ | Ως3Άρ‘Σ |
““ΙΪΥΨ | ”·3Άρ‘Σ | Ως3.5Άρ‘Σ |
Θ®1Θ©Ζ÷±π«σΦΉΓΔ““ΝΫΗωΙΪΥΨ’β100Χλ…ζ≤ζΒΡ≤ζΤΖΒΡ’ΐΤΖ¬ Θ®”ΟΑΌΖ÷ ΐ±μ ΨΘ©.
Θ®2Θ© ‘Έ ΦΉΓΔ““ΝΫΗωΙΪΥΨ’β100Χλ…ζ≤ζΒΡ≤ζΤΖΒΡΉήάϊ»σΡΡΗωΗϋ¥σΘΩΥΒΟςάμ”….
Θ®3Θ©»τ“‘ΦΉΙΪΥΨ’β100Χλ÷–ΟΩΧλ≤ζΤΖάϊ»σΉήΚΆΕ‘”ΠΒΡΤΒ¬ ΉςΈΣΗ≈¬ Θ§¥”ΦΉΙΪΥΨ’β100ΧλΥφΜζ≥ι»Γ1ΧλΘ§Φ«’βΧλ≤ζΤΖάϊ»σΉήΚΆΈΣXΘ§«σXΒΡΖ÷≤ΦΝ–ΦΑΤδ ΐ―ßΤΎΆϊ.