题目内容
【题目】椭圆![]() 的右焦点为F到直线
的右焦点为F到直线![]() 的距离为
的距离为![]() ,抛物线
,抛物线![]() 的焦点与椭圆E的焦点F重合,过F作与x轴垂直的直线交椭圆于S,T两点,交抛物线于C,D两点,且
的焦点与椭圆E的焦点F重合,过F作与x轴垂直的直线交椭圆于S,T两点,交抛物线于C,D两点,且![]() .
.
(1)求椭圆E及抛物线G的方程;
(2)过点F且斜率为k的直线l交椭圆于A,B点,交抛物线于M,N两点,如图所示,请问是否存在实常数![]() ,使
,使![]() 为常数,若存在,求出
为常数,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.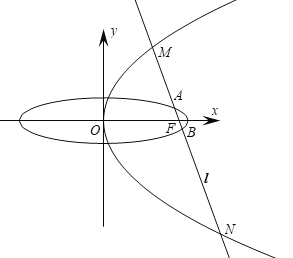
【答案】(1)椭圆方程为![]() ,抛物线G的方程为
,抛物线G的方程为![]() ;(2)存在
;(2)存在![]() ,理由见解析.
,理由见解析.
【解析】
(1)设椭圆于抛物线的公共焦点![]() ,根据右焦点F到直线
,根据右焦点F到直线![]() 的距离为
的距离为![]() ,得到
,得到![]() ,解得
,解得![]() ,再由
,再由![]() ,即
,即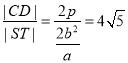 ,解得a,b即可.
,解得a,b即可.
(2)设![]() ,直线l的方程
,直线l的方程![]() 与椭圆方程,抛物线方程分别联立,利用弦长公式分别求得
与椭圆方程,抛物线方程分别联立,利用弦长公式分别求得 ![]() ,
,![]() ,代入
,代入![]() 分析求解.
分析求解.
(1)设椭圆与抛物线的公共焦点![]() ,
,
因为F到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,
解得![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以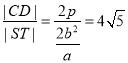 ,
,
所以![]() ,又
,又![]() ,
,
解得![]() ,
,
所以椭圆方程为![]() ,抛物线G的方程为
,抛物线G的方程为![]() .
.
(2)设![]() ,
,
设直线l的方程为:![]() ,与椭圆方程联立消去y得:
,与椭圆方程联立消去y得:![]() ,
,
所以![]() ,
,
所以![]()
![]() .
.
直线l的方程![]() 与抛物线方程联立消去y得:
与抛物线方程联立消去y得:
![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以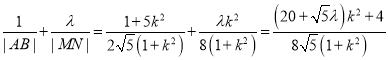 ,
,
要使![]() 为常数,则
为常数,则![]() ,解得
,解得![]() .
.
故存在![]() 使得
使得![]() 为常数.
为常数.

【题目】某村为了脱贫致富,引进了两种麻鸭品种,一种是旱养培育的品种,另一种是水养培育的品种.为了了解养殖两种麻鸭的经济效果情况,从中随机抽取500只麻鸭统计了它们一个季度的产蛋量(单位:个),制成了如图的频率分布直方图,且已知麻鸭的产蛋量在![]() 的频率为0.66.
的频率为0.66.
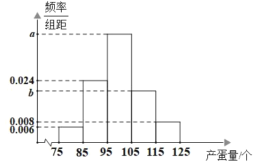
(1)求![]() ,
,![]() 的值;
的值;
(2)已知本次产蛋量近似服从![]() (其中
(其中![]() 近似为样本平均数,
近似为样本平均数,![]() 似为样本方差).若本村约有10000只麻鸭,试估计产蛋量在110~120的麻鸭数量(以各组区间的中点值代表该组的取值).
似为样本方差).若本村约有10000只麻鸭,试估计产蛋量在110~120的麻鸭数量(以各组区间的中点值代表该组的取值).
(3)若以正常产蛋90个为标准,大于90个认为是良种,小于90个认为是次种.根据统计得出两种培育方法的![]() 列联表如下,请完成表格中的统计数据,并判断是否有99.5%的把握认为产蛋量与培育方法有关.
列联表如下,请完成表格中的统计数据,并判断是否有99.5%的把握认为产蛋量与培育方法有关.
良种 | 次种 | 总计 | |
旱养培育 | 160 | 260 | |
水养培育 | 60 | ||
总计 | 340 | 500 |
附:![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
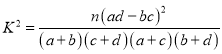 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |