题目内容
如图,平面直角坐标系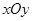 中,已知向量
中,已知向量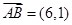 ,
,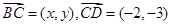 ,且
,且 。
。
(1)求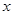 与
与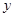 间的关系;(2)若
间的关系;(2)若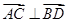 ,求
,求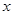 与
与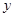 的值及四边形
的值及四边形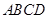 的面积.
的面积.
(1)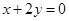 ;(2)
;(2)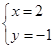 或
或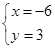 ,
,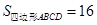 .
.
解析试题分析:(1)先求出 的坐标,
的坐标,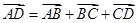 ,代入相应坐标即可得到
,代入相应坐标即可得到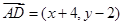 ,进而由
,进而由 得到
得到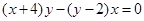 ,整理即可得到
,整理即可得到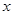 与
与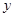 的关系式;(2)先由
的关系式;(2)先由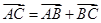 、
、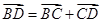 算出
算出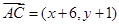 、
、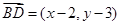 ,再由
,再由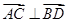 得到
得到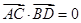 即
即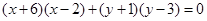 ,化简
,化简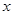 、
、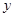 的另一个关系式,联立两个
的另一个关系式,联立两个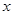 、
、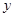 的关系式,求解即可得到
的关系式,求解即可得到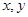 的取值,进而确定
的取值,进而确定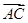 、
、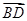 ,再由
,再由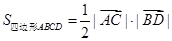 算出四边形
算出四边形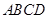 的面积即可.
的面积即可.
试题解析:(1)由题意得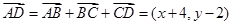 ,
,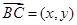
因为 ,所以
,所以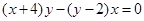 ,即
,即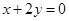 ①
①
(2)由题意得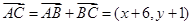 ,
,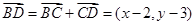
因为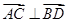 ,所以
,所以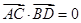 即
即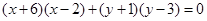 ,即
,即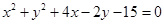 ②
②
由①②得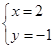 或
或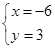
当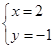 时,
时,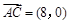 ,
,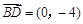 ,则
,则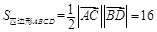
当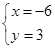 时,
时,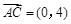 ,
, ,则
,则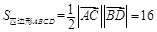
所以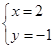 或
或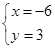 ,四边形
,四边形 的面积为16.
的面积为16.
考点:1.平面向量的线性运算;2.平面向量的坐标运算;3.平面向量的数量积;4.平面向量平行、垂直的判定与性质.

练习册系列答案
相关题目
已知数列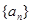 的前
的前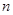 项和为
项和为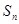 ,且
,且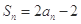 则
则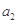 等于( )
等于( )
| A.4 | B.2 | C.1 | D.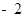 |
 ,则动点P(x,y)的轨迹方程为 .
,则动点P(x,y)的轨迹方程为 .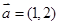 ,
, ,当
,当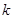 为何值时,
为何值时,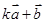 与
与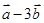 垂直?(2)
垂直?(2)  与
与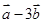 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?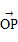 =
=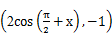 ,
,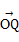 =
=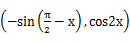 ,定义函数f(x)=
,定义函数f(x)=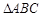 中,
中,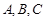 的对边分别是
的对边分别是 ,已知
,已知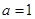 ,平面向量
,平面向量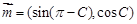 ,
,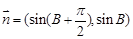 ,且
,且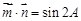 .
.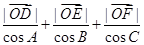 的值.
的值.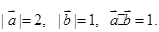
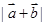 的值; (2)若
的值; (2)若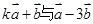 垂直,求
垂直,求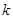 的值.
的值.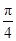 ,求当|m|取最小值时实数t的值;
,求当|m|取最小值时实数t的值;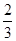 ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由. ,点
,点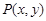 为直线
为直线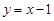 上的一个动点.
上的一个动点. 恒为锐角;
恒为锐角; 为菱形,求
为菱形,求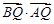 的值.
的值.