题目内容
已知向量a="(1,2),b=(cos" α,sin α),设m=a+tb(t为实数).
(1)若α=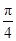 ,求当|m|取最小值时实数t的值;
,求当|m|取最小值时实数t的值;
(2)若a⊥b,问:是否存在实数t,使得向量a-b和向量m夹角的余弦值为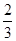 ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由.
(1)  (2) 存在t=1或t=-7满足条件
(2) 存在t=1或t=-7满足条件
解析解:(1)因为α=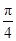 ,
,
所以b=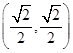 ,a·b=
,a·b= ,
,
则|m|=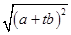
=
=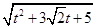
= ,
,
所以当t=- 时,|m|取到最小值,最小值为
时,|m|取到最小值,最小值为 .
.
(2)存在实数t满足条件,理由如下:
由条件得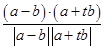 =
=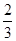 ,
,
又因为|a-b|=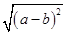 =
=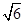 ,
,
|a+tb|=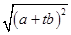 =
= ,
,
(a-b)·(a+tb)=5-t,
所以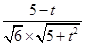
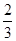 =,且t<5,
=,且t<5,
整理得t2+6t-7=0,
所以存在t=1或t=-7满足条件.

练习册系列答案
相关题目
已知向量a=(1,2),b=(-2,m),x=a+(t2+1)b,y=-ka+ b,m∈R,k、t为正实数.
b,m∈R,k、t为正实数.
(1)若a∥b,求m的值;
(2)若a⊥b,求m的值;
(3)当m=1时,若x⊥y,求k的最小值.
已知数列:2,0,2,0,2,0, .前六项不适合下列哪个通项公式
A. =1+(―1)n+1 =1+(―1)n+1 | B. =2|sin =2|sin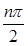 | | |
C. =1-(―1)n =1-(―1)n | D. =2sin =2sin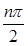 |
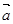 ,
,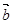 的夹角为
的夹角为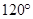 ,且
,且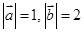 ,则向量
,则向量 在向量
在向量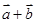 方向上的投影是 ________.
方向上的投影是 ________. =2a-b,
=2a-b, =3a+b,
=3a+b,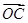 =a-3b,求证:A、B、C三点共线;
=a-3b,求证:A、B、C三点共线;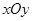 中,已知向量
中,已知向量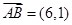 ,
,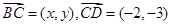 ,且
,且 。
。
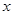 与
与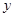 间的关系;(2)若
间的关系;(2)若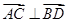 ,求
,求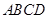 的面积.
的面积. 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i.
对应的复数为3-i.
 (;(2)
(;(2)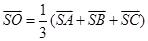 .
.