题目内容
已知双曲线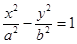 的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于
的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于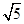 ,则该双曲线的方程为
,则该双曲线的方程为
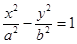 的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于
的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于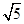 ,则该双曲线的方程为
,则该双曲线的方程为A.5x2-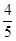 y2=1? y2=1? | B.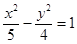 |
C.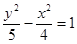 | D.5x2-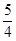 y2=1 y2=1 |
D
先根据抛物线方程求得焦点坐标,进而确定双曲线的焦点,求得双曲线中的c,根据离心率进而求得长半轴,最后根据b2=c2-a2求得b,则双曲线的方程可得.
解:抛物线y2=4x的焦点F(1,0),
c=1,e=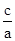 =
=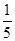 ,a2=
,a2=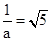 ,b2=c2-a2=
,b2=c2-a2=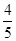 双曲线的方程为5x2-
双曲线的方程为5x2-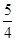 y2=1
y2=1
故选D
解:抛物线y2=4x的焦点F(1,0),
c=1,e=
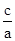 =
=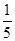 ,a2=
,a2=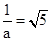 ,b2=c2-a2=
,b2=c2-a2=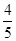 双曲线的方程为5x2-
双曲线的方程为5x2-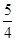 y2=1
y2=1故选D

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
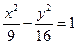 的右焦点F作倾斜角为的直线交双曲线于A、B两点,求线段AB的中点C到焦点F的距离
的右焦点F作倾斜角为的直线交双曲线于A、B两点,求线段AB的中点C到焦点F的距离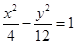 的焦点到渐近线的距离为( )
的焦点到渐近线的距离为( )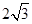
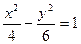 右焦点的直线与双曲线相交得弦长为
右焦点的直线与双曲线相交得弦长为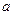 ,若这样的直线恰有两条,则
,若这样的直线恰有两条,则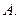 4
4  5
5 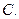 6
6 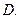 7
7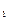 ,F
,F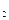 分别是双曲线C:
分别是双曲线C: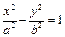 的左.右焦点,过F
的左.右焦点,过F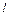 与双曲线的左支相交于A\B两点,且
与双曲线的左支相交于A\B两点,且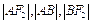 成等差数列,则双曲线的离心率为 .
成等差数列,则双曲线的离心率为 .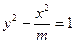 的虚轴长是实轴长的2倍,则m= .
的虚轴长是实轴长的2倍,则m= .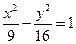 ,
,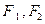 分别为它的
分别为它的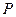 为双曲线上一点,设
为双曲线上一点,设 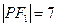 ,
,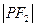 的值为 ▲ .
的值为 ▲ .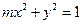 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则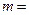 .
.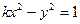 的一条渐近线与直线
的一条渐近线与直线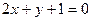 垂直,那么双曲线的离心 率为 ;渐近线方程为
垂直,那么双曲线的离心 率为 ;渐近线方程为