题目内容
已知一袋有2个白球和4个黑球。
(1)采用不放回地从袋中摸球(每次摸一球),4次摸球,求恰好摸到2个黑球的概率;
(2)采用有放回从袋中摸球(每次摸一球),4次摸球,令X表示摸到黑球次数,
求X的分布列和期望.
(1)采用不放回地从袋中摸球(每次摸一球),4次摸球,求恰好摸到2个黑球的概率;
(2)采用有放回从袋中摸球(每次摸一球),4次摸球,令X表示摸到黑球次数,
求X的分布列和期望.
(1)、
(2)

(2)

本试题主要是考查了古典概型概率和随机变量的分布列以及数学期望值的求解,二项分布的运用。
(1)因为一袋有2个白球和4个黑球。采用不放回地从袋中摸球(每次摸一球),4次摸球,求恰好摸到2个黑球直接利用古典概型概率公式计算得到。
(2)由于是由放回的摸球,因此是独立重复试验,运用其公式可以解得。
解:(1)、
(2)、X可取0,1,2,3,4
一次摸球为黑球的概率
 ,
,


(1)因为一袋有2个白球和4个黑球。采用不放回地从袋中摸球(每次摸一球),4次摸球,求恰好摸到2个黑球直接利用古典概型概率公式计算得到。
(2)由于是由放回的摸球,因此是独立重复试验,运用其公式可以解得。
解:(1)、

(2)、X可取0,1,2,3,4
一次摸球为黑球的概率
 ,
,



练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 表示这7条鱼中被QQ先生吃掉的鱼的条数,求
表示这7条鱼中被QQ先生吃掉的鱼的条数,求 .
. 2列联表:
2列联表: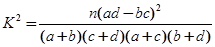 其中n=a+b+c+d
其中n=a+b+c+d

 ,求
,求 的值.
的值.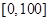 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
. 的值;
的值; ,求
,求 视觉
视觉 

 .
. ,求随机变量
,求随机变量 .
. ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
.
 的数学期望;
的数学期望;