题目内容
QQ先生的鱼缸中有7条鱼,其中6条青鱼和1条黑鱼,计划从当天开始,每天中午从该鱼缸中抓出1条鱼(每条鱼被抓到的概率相同)并吃掉.若黑鱼未被抓出,则它每晚要吃掉1条青鱼(规定青鱼不吃鱼).
(Ⅰ)求这7条鱼中至少有6条被QQ先生吃掉的概率;
(Ⅱ)以 表示这7条鱼中被QQ先生吃掉的鱼的条数,求
表示这7条鱼中被QQ先生吃掉的鱼的条数,求 的分布列及其数学期望
的分布列及其数学期望 .
.
(Ⅰ)求这7条鱼中至少有6条被QQ先生吃掉的概率;
(Ⅱ)以
 表示这7条鱼中被QQ先生吃掉的鱼的条数,求
表示这7条鱼中被QQ先生吃掉的鱼的条数,求 的分布列及其数学期望
的分布列及其数学期望 .
.(Ⅰ) 先生至少吃掉6条鱼的概率是
先生至少吃掉6条鱼的概率是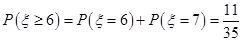
(Ⅱ) 的分布列为
的分布列为
故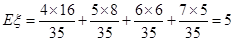 ,所求期望值为5.
,所求期望值为5.
 先生至少吃掉6条鱼的概率是
先生至少吃掉6条鱼的概率是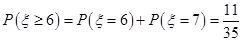
(Ⅱ)
 的分布列为
的分布列为 | 4 | 5 | 6 | 7 |
| P | 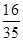 | 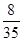 | 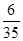 | 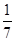 |
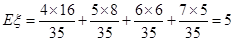 ,所求期望值为5.
,所求期望值为5. 本试题主要是考查了独立事件的概率的乘法公式的运用
(1)利用独立事件的概率的乘法公式可知设QQ先生能吃到的鱼的条数为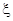
QQ先生要想吃到7条鱼就必须在第一天吃掉黑鱼,概率为1/7.
(2因为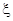 的可能取值为4,5,6,7,那么最坏的情况是只能吃到4条鱼:前3天各吃掉1条青鱼,其余3条青鱼被黑鱼吃掉, 第4天QQ先生吃掉黑鱼,其概率可以求解得到,从而得到分布列和数学期望。
的可能取值为4,5,6,7,那么最坏的情况是只能吃到4条鱼:前3天各吃掉1条青鱼,其余3条青鱼被黑鱼吃掉, 第4天QQ先生吃掉黑鱼,其概率可以求解得到,从而得到分布列和数学期望。
(1)利用独立事件的概率的乘法公式可知设QQ先生能吃到的鱼的条数为
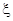
QQ先生要想吃到7条鱼就必须在第一天吃掉黑鱼,概率为1/7.
(2因为
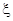 的可能取值为4,5,6,7,那么最坏的情况是只能吃到4条鱼:前3天各吃掉1条青鱼,其余3条青鱼被黑鱼吃掉, 第4天QQ先生吃掉黑鱼,其概率可以求解得到,从而得到分布列和数学期望。
的可能取值为4,5,6,7,那么最坏的情况是只能吃到4条鱼:前3天各吃掉1条青鱼,其余3条青鱼被黑鱼吃掉, 第4天QQ先生吃掉黑鱼,其概率可以求解得到,从而得到分布列和数学期望。
练习册系列答案
相关题目
 (
( 、
、 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表: 四个不同的岗位服务,每个岗位至少有一名志愿者,设随机变量
四个不同的岗位服务,每个岗位至少有一名志愿者,设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,则
岗位服务的人数,则 _
_ =____________.
=____________. 表示取出的球的最大号码,则
表示取出的球的最大号码,则 ( )
( ) 







