题目内容
(本小题满分12分)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是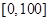 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
.
(Ⅰ)求直方图中 的值;
的值;
(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,
请估计学校600名新生中有多少名学生可以申请住宿;
(Ⅲ)从学校的新生中任选4名学生,这4名学生中上学所需时间
少于20分钟的人数记为 ,求
,求 的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)
的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)
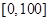 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
.(Ⅰ)求直方图中
 的值;
的值;(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,
请估计学校600名新生中有多少名学生可以申请住宿;
(Ⅲ)从学校的新生中任选4名学生,这4名学生中上学所需时间
少于20分钟的人数记为
 ,求
,求 的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)
的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)(Ⅰ) . (Ⅱ)以600名新生中有72名学生可以申请住宿.
. (Ⅱ)以600名新生中有72名学生可以申请住宿.
(Ⅲ) 的分布列为:
的分布列为:
 .(或
.(或 )
)
所以 的数学期望为1.
的数学期望为1.
 . (Ⅱ)以600名新生中有72名学生可以申请住宿.
. (Ⅱ)以600名新生中有72名学生可以申请住宿. (Ⅲ)
 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 | 4 |
 |  |  |  |  |  |
 .(或
.(或 )
)所以
 的数学期望为1.
的数学期望为1. 本试题主要是考查了直方图的运用,求解频率和古典概型概率的计算、分布列和期望值的综合运用。
(1)由直方图可得: .
.
所以 .
.
(2)新生上学所需时间不少于1小时的频率为: , …4分
, …4分
因为 ,所以600名新生中有72名学生可以申请住宿
,所以600名新生中有72名学生可以申请住宿
(3)因为由直方图可知,每位学生上学所需时间少于20分钟的概率为 ,
,
和随机变量的各个取值,得到分布列和期望值。
解:(Ⅰ)由直方图可得: .
.
所以 . ………………………………………2分
. ………………………………………2分
(Ⅱ)新生上学所需时间不少于1小时的频率为: , …4分
, …4分
因为 ,所以600名新生中有72名学生可以申请住宿. …5分
,所以600名新生中有72名学生可以申请住宿. …5分
(Ⅲ) 的可能取值为0,1,2,3,4. ………………………………………6分
的可能取值为0,1,2,3,4. ………………………………………6分
由直方图可知,每位学生上学所需时间少于20分钟的概率为 ,
,
 ,
,  ,
,
 ,
, ,
,
 . ………………………10分
. ………………………10分
所以 的分布列为:
的分布列为:
 .(或
.(或 )
)
所以 的数学期望为1. ………………………………………12分
的数学期望为1. ………………………………………12分
(1)由直方图可得:
 .
.所以
 .
.(2)新生上学所需时间不少于1小时的频率为:
 , …4分
, …4分因为
 ,所以600名新生中有72名学生可以申请住宿
,所以600名新生中有72名学生可以申请住宿(3)因为由直方图可知,每位学生上学所需时间少于20分钟的概率为
 ,
,和随机变量的各个取值,得到分布列和期望值。
解:(Ⅰ)由直方图可得:
 .
.所以
 . ………………………………………2分
. ………………………………………2分(Ⅱ)新生上学所需时间不少于1小时的频率为:
 , …4分
, …4分因为
 ,所以600名新生中有72名学生可以申请住宿. …5分
,所以600名新生中有72名学生可以申请住宿. …5分(Ⅲ)
 的可能取值为0,1,2,3,4. ………………………………………6分
的可能取值为0,1,2,3,4. ………………………………………6分由直方图可知,每位学生上学所需时间少于20分钟的概率为
 ,
, ,
,  ,
, ,
, ,
, . ………………………10分
. ………………………10分所以
 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 | 4 |
 |  |  |  |  |  |
 .(或
.(或 )
)所以
 的数学期望为1. ………………………………………12分
的数学期望为1. ………………………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 =____________.
=____________. 两个项目,投资
两个项目,投资 项目
项目 万元,一年后获得的利润为随机变量
万元,一年后获得的利润为随机变量 (万元),根据市场分析,
(万元),根据市场分析,
 项目
项目 (万元)与
(万元)与 次独立的调整,且在每次调整中价格下调的概率都是
次独立的调整,且在每次调整中价格下调的概率都是 .
.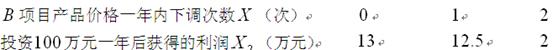
 ;
; ,根据投资获得利润的差异,你愿意选择投资哪个项目?
,根据投资获得利润的差异,你愿意选择投资哪个项目? ).
). 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
. 的概率;
的概率; 个点,连续取
个点,连续取 次,得到
次,得到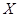 ,求
,求 的分布列和数学期望.
的分布列和数学期望. 表示取出的球的最大号码,则
表示取出的球的最大号码,则 ( )
( ) 

 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 .
. 的概率分布列如下,且
的概率分布列如下,且 则
则