题目内容
16.若函数f(x)=2x2-lnx在区间(k-1,k+1)内有定义且不是单调函数,则实数k的取值范围为$1≤k<\frac{3}{2}$.分析 先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解方程fˊ(x)=0,使方程的解在定义域内的一个子区间(k-1,k+1)内,建立不等关系,解之即可.
解答 解:f(x)定义域为(0,+∞),f′(x)=4x-$\frac{1}{x}$,
由f'(x)=0,得x=$\frac{1}{2}$.
当x∈(0,$\frac{1}{2}$)时,f'(x)<0,当x∈($\frac{1}{2}$,+∞)时,f'(x)>0
据题意,0≤k-1<$\frac{1}{2}$<k+1,
解得$1≤k<\frac{3}{2}$.
故答案为:$1≤k<\frac{3}{2}$.
点评 本题主要考查了对数函数的导数,以及利用导数研究函数的单调性等基础知识,考查计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.对于R上可导的任意函数f(x),若满足(x-2)f′(x)≥0,则必有( )
| A. | f(0)+f(3)<2f(2) | B. | f(0)+f(3)≤2f(2) | C. | f(0)+f(3)≥2f(2) | D. | f(0)+f(3)>2f(2) |
6.各项都为正数的等比数列{an}中,a1a9=10,则a5的值为( )
| A. | 5 | B. | ±$\sqrt{10}$ | C. | $\sqrt{10}$ | D. | -5 |
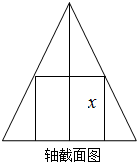 一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱:
一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱: