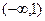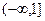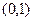题目内容
(本小题满分12分)已知二次函数 的
的 图象以原点为顶点且过点(1,1),反比例函数
图象以原点为顶点且过点(1,1),反比例函数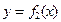 的图象与直线
的图象与直线 的两个交点间的距离为8,
的两个交点间的距离为8,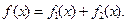
(1)求函数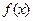 的表达式;
的表达式;
(2)证明:当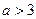 时,关于
时,关于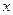 的方程
的方程 有三个实数解.
有三个实数解.
 的
的 图象以原点为顶点且过点(1,1),反比例函数
图象以原点为顶点且过点(1,1),反比例函数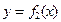 的图象与直线
的图象与直线 的两个交点间的距离为8,
的两个交点间的距离为8,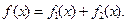
(1)求函数
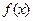 的表达式;
的表达式;(2)证明:当
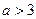 时,关于
时,关于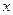 的方程
的方程 有三个实数解.
有三个实数解.(1)由已知,设 ,由
,由
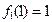 ,得
,得 ,∴
,∴ ……2分
……2分
设 ,它的图象与直线
,它的图象与直线 的交点分别为
的交点分别为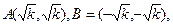
由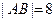 ,得
,得
∴ 故
故 ……4分
……4分
(2)证明:由 ,得
,得
即 ……5分
……5分
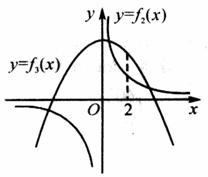
在同一坐标系内作出 和
和 的大致图象如图,其中
的大致图象如图,其中 的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线,
的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线, 的图象是以
的图象是以 为顶点,开口向下的抛物线.
为顶点,开口向下的抛物线.
∴
 与
与 的图象在第三象限有一个交点,
的图象在第三象限有一个交点,
即 有一个负数解.…… 8分
有一个负数解.…… 8分
又∵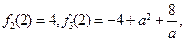
当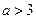
 时,
时,
∴当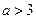 时,在第一象限
时,在第一象限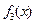 的图象上存在一点
的图象上存在一点 在
在 图象的上方.
图象的上方.
∴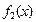 与
与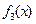 的图象在第一象限有两个交点,
的图象在第一象限有两个交点,
即 有两个正数解.
有两个正数解.
∴方程 有三个实数解.…… 12分
有三个实数解.…… 12分
 ,由
,由
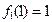 ,得
,得 ,∴
,∴ ……2分
……2分设
 ,它的图象与直线
,它的图象与直线 的交点分别为
的交点分别为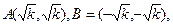
由
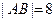 ,得
,得
∴
 故
故 ……4分
……4分(2)证明:由
 ,得
,得
即
 ……5分
……5分在同一坐标系内作出
 和
和 的大致图象如图,其中
的大致图象如图,其中 的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线,
的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线,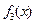 的图象是以
的图象是以 为顶点,开口向下的抛物线.
为顶点,开口向下的抛物线.
∴

 与
与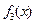 的图象在第三象限有一个交点,
的图象在第三象限有一个交点,即
 有一个负数解.…… 8分
有一个负数解.…… 8分又∵
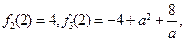
当
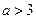
 时,
时,
∴当
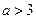 时,在第一象限
时,在第一象限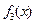 的图象上存在一点
的图象上存在一点 在
在 图象的上方.
图象的上方.∴
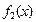 与
与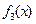 的图象在第一象限有两个交点,
的图象在第一象限有两个交点,即
 有两个正数解.
有两个正数解.∴方程
 有三个实数解.…… 12分
有三个实数解.…… 12分略

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
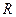 的函数
的函数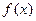 满足
满足 .
.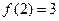 ,求
,求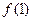 ;又若
;又若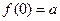 ,求
,求 ;
; ,使得
,使得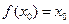 ,求函数
,求函数 满足
满足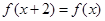 且
且 时
时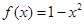 ,函数
,函数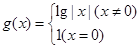 ,则函数
,则函数 在区间
在区间 内零点的个数为( )
内零点的个数为( )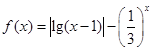 有两个零点x1,x2,则有
有两个零点x1,x2,则有

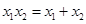

 ,则关于
,则关于 的方程
的方程 有7个不同实数解的充要条件是( )
有7个不同实数解的充要条件是( ) 且
且
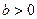 且
且
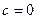
 且
且 的图像的对称中心为
的图像的对称中心为 ,则实数
,则实数 的值为( )
的值为( )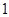
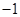


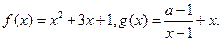
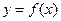 和
和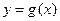 的公共点个数;
的公共点个数;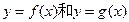 的公共点个数恰为两个。
的公共点个数恰为两个。 的零点所在的区间为( )
的零点所在的区间为( )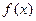 的定义域为R,且
的定义域为R,且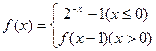 若方程
若方程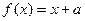 有两不同实根,则a的取值范围为 ( )
有两不同实根,则a的取值范围为 ( )