题目内容
当p1,p2,…,pn均为正数时,称| n |
| p1+p2+…+pn |
| 1 |
| 2n+1 |
(Ⅰ)试求数列{an}的通项公式;
(Ⅱ)设cn=
| an |
| 2n+1 |
(Ⅲ)已知bn=tan(t>0),记数列{bn}的前n项和为Sn,试求
| Sn+1 |
| Sn |
分析:(Ⅰ)先利用条件求得a1+a2++an-1+an=n(2n+1)和a1+a2++an-1=(n-1)(2n-1),两式作差就可求出数列{an}的通项公式(注意检验n=1是否成立);
(Ⅱ)利用 (Ⅰ)求得的数列{an}的通项公式代入即可求出cn+1-cn再利用函数的单调性就可判断出cn+1-cn(n∈N*)的符号;
(Ⅲ)利用 (Ⅰ)求得的数列{an}的通项公式代入即可求出数列{bn}的通项公式,再对等比数列{bn}分公比等于1和不等于1两种情况分别求和即可找到
的值;
(Ⅱ)利用 (Ⅰ)求得的数列{an}的通项公式代入即可求出cn+1-cn再利用函数的单调性就可判断出cn+1-cn(n∈N*)的符号;
(Ⅲ)利用 (Ⅰ)求得的数列{an}的通项公式代入即可求出数列{bn}的通项公式,再对等比数列{bn}分公比等于1和不等于1两种情况分别求和即可找到
| Sn+1 |
| Sn |
解答:解:(Ⅰ)由题得:a1+a2+…+an-1+an=n(2n+1) ①,
a1+a2+…+an-1=(n-1)(2n-1) ②,
两式相减,得an=4n-1(n≥2)
又
=
,解得a1=3=4×1-1,
∴an=4n-1(n∈N+).
(Ⅱ)∵cn=
=
=2-
,cn+1=
=2-
,
∴cn+1-cn=
-
>0,即cn+1>cn.
(Ⅲ)∵bn=tan=t4n-1(t>0),
∴Sn=b1+b2++bn=t3+t7++t4n-1,
当t=1时,Sn=n,
=
;
当t>0且t≠1时,Sn=
,
=
.
综上得,
=
a1+a2+…+an-1=(n-1)(2n-1) ②,
两式相减,得an=4n-1(n≥2)
又
| 1 |
| a1 |
| 1 |
| 2×1+1 |
∴an=4n-1(n∈N+).
(Ⅱ)∵cn=
| an |
| 2n+1 |
| 4n-1 |
| 2n+1 |
| 3 |
| 2n+1 |
| an+1 |
| 2n+3 |
| 3 |
| 2n+3 |
∴cn+1-cn=
| 3 |
| 2n+1 |
| 3 |
| 2n+3 |
(Ⅲ)∵bn=tan=t4n-1(t>0),
∴Sn=b1+b2++bn=t3+t7++t4n-1,
当t=1时,Sn=n,
| Sn+1 |
| Sn |
| n+1 |
| n |
当t>0且t≠1时,Sn=
| t3(1-t4n) |
| 1-t4 |
| Sn+1 |
| Sn |
| 1-t4n+4 |
| 1-t4n |
综上得,
| Sn+1 |
| Sn |
|
点评:本题在利用新定义的条件下考查数列的通项公式以及求和公式,还有利用函数的单调性判断函数值的符号.是一道综合性很强的好题.

练习册系列答案
相关题目
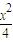 -
-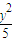 =1(x>2),O是坐标原点.
=1(x>2),O是坐标原点.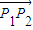 所成的比为λ(λ>0),当λ∈[
所成的比为λ(λ>0),当λ∈[ ,
, ]时,求|
]时,求|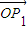 |•|
|•|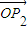 |的最值.
|的最值.