Question

（09年湖北鄂州5月模拟理）已知两定点A(－3，0)，B(3，0)，动圆M与直线AB相切于点N，且，现分别过点A、B作动圆M的切线（异于直线AB），两切线相交于点P．

⑴求动点P的轨迹方程；

⑵若直线xmy3＝0截动点P的轨迹所得的弦长为5，求m的值；

    ⑶设过轨迹上的点P的直线与两直线分别交于点P₁、P₂，且点P分有向线段所成的比为λ(λ＞0)，当λ∈时，求的最值．

Answer 1

解析：⑴由题设及平面几何知识得

∴动点P的轨迹是以A、B为焦点的双曲线右支由，

∴b²＝c²－a²＝5，故所求P点的轨迹方程为                3分

⑵易知直线xmy3＝0恒过双曲线焦点B(3，0)

设该直线与双曲线右支相交于D(x_D，y_D)，E(x_E，y_E)由双曲线第二定义知

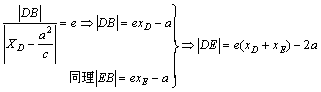，又a＝2，c＝3，

∴e＝则                                                               5分

由|DE|＝5，得，从而易知仅当m＝0时，满足|DE|＝5

故所求m＝0                                                                                           7分

⑶设P(x，y)，P₁(x₁、y₁)，P₂(x₂、y₂)且P分有向线段所成的比为λ，则

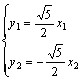，又点P(x，y)在双曲线

上，∴，化简得，

又，，∴         9分

令  ∵在上单减，在上单增，

又    ∴在上单减，在上单增，∴u_min＝u(1)＝4，

又，    ∴u_min＝

故的最小值为9，最大值为。