题目内容
已知动点P的轨迹方程为:
-
=1(x>2),O是坐标原点.
①若直线x-my-3=0截动点P的轨迹所得弦长为5,求实数m的值;
②设过P的轨迹上的点P的直线与该双曲线的两渐近线分别交于点P1、P2,且点P分有向线段
所成的比为λ(λ>0),当λ∈[
,
]时,求|
|•|
|的最值.
| x2 |
| 4 |
| y2 |
| 5 |
①若直线x-my-3=0截动点P的轨迹所得弦长为5,求实数m的值;
②设过P的轨迹上的点P的直线与该双曲线的两渐近线分别交于点P1、P2,且点P分有向线段
| P1P2 |
| 3 |
| 4 |
| 3 |
| 2 |
| OP1 |
| OP2 |
分析:①先确定直线与双曲线的右支相交,设两个交点坐标分别为D(xD,yD)、E(xE,yE),由双曲线的第二定义,求出|DF|、|EF|,从而可得|DE|,利用直线x-my-3=0截动点P的轨迹所得弦长为5,即可求得m的值;
②先确定P的坐标,进而可表示|
|•|
|,利用基本不等式及端点的函数值,即可求得|
|•|
|的最值.
②先确定P的坐标,进而可表示|
| OP1 |
| OP2 |
| OP1 |
| OP2 |
解答:解:①由动点P的轨迹方程为:
-
=1(x>2),∴直线x-my-3=0恒过双曲线的右焦点F(3,0),于是直线与双曲线的右支相交,
设两个交点坐标分别为D(xD,yD)、E(xE,yE),
由双曲线的第二定义得
=e,∴|DF|=exD-a
同理|EF|=exE-a,∴|DE|=e(xD+xE)-2a
∵a=2,c=3,∴e=
,∴|DE|=
(xD+xE)-4
∵若直线x-my-3=0截动点P的轨迹所得弦长为5
∴
(xD+xE)-4=5
∴xD+xE=6
由直线过右焦点F(3,0),知xD=xE=3,此时直线垂直于x轴,∴m=0.
②设P(x,y),P1(x1,y1),P2(x2,y2),则
∴x=
,y=
=
×
∵点P(x,y)在双曲线:
-
=1上
∴
-
×
=1,化简可得x1x2=
∵|
|=
|x1|,|
|=
|x2|
∴|
|•|
|=
|x1x2|=
×
令u=
=λ+
+2
∵λ∈[
,
],∴λ=1时,λ+
+2取得最小值4
∵λ=
时,u=
,λ=
时,u=
,∴λ+
+2的最大值为
∴|
|•|
|的最小值为9,最大值为
.
| x2 |
| 4 |
| y2 |
| 5 |
设两个交点坐标分别为D(xD,yD)、E(xE,yE),
由双曲线的第二定义得
| |DF| | ||
|xD-
|
同理|EF|=exE-a,∴|DE|=e(xD+xE)-2a
∵a=2,c=3,∴e=
| 3 |
| 2 |
| 3 |
| 2 |
∵若直线x-my-3=0截动点P的轨迹所得弦长为5
∴
| 3 |
| 2 |
∴xD+xE=6
由直线过右焦点F(3,0),知xD=xE=3,此时直线垂直于x轴,∴m=0.
②设P(x,y),P1(x1,y1),P2(x2,y2),则
|
∴x=
| x1+λx2 |
| 1+λ |
| y1+λy2 |
| 1+λ |
| ||
| 2 |
| x1-λx2 |
| 1+λ |
∵点P(x,y)在双曲线:
| x2 |
| 4 |
| y2 |
| 5 |
∴
| (x1+λx2)2 |
| 4(1+λ)2 |
| 5 |
| 4 |
| (x1-λx2)2 |
| 5(1+λ)2 |
| (1+λ)2 |
| λ |
∵|
| OP1 |
| 3 |
| 2 |
| OP2 |
| 3 |
| 2 |
∴|
| OP1 |
| OP2 |
| 9 |
| 4 |
| 9 |
| 4 |
| (1+λ)2 |
| λ |
令u=
| (1+λ)2 |
| λ |
| 1 |
| λ |
∵λ∈[
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| λ |
∵λ=
| 3 |
| 4 |
| 49 |
| 12 |
| 3 |
| 2 |
| 25 |
| 6 |
| 1 |
| λ |
| 25 |
| 6 |
∴|
| OP1 |
| OP2 |
| 75 |
| 8 |
点评:本题考查直线与双曲线的位置关系的综合应用,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
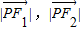 的等差中项为
的等差中项为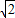 .
.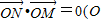 为坐标原点),求直线l的方程;
为坐标原点),求直线l的方程;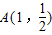 ,点P为曲线C上任意一点,求
,点P为曲线C上任意一点,求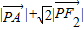 的最小值,并求取得最小值时点P的坐标.
的最小值,并求取得最小值时点P的坐标.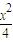 -
-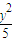 =1(x>2),O是坐标原点.
=1(x>2),O是坐标原点.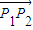 所成的比为λ(λ>0),当λ∈[
所成的比为λ(λ>0),当λ∈[ ,
, ]时,求|
]时,求|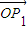 |•|
|•|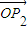 |的最值.
|的最值.