题目内容
【题目】已知函数f(x)=|2x﹣1|﹣|x﹣3|.
(Ⅰ)解不等式f(x)≥1;
(Ⅱ)当﹣9≤x≤4时,不等式f(x)<a成立,求实数a的取值范围.
【答案】解:(Ⅰ)∵|2x﹣1|﹣|x﹣3|≥1, ∴ ![]() 或
或 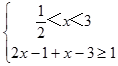 或
或 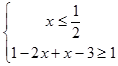 ,
,
解得:x≥ ![]() 或x≤﹣3,
或x≤﹣3,
故不等式的解集是: ![]() .
.
(Ⅱ)f(x)=|2x﹣1|﹣|x﹣3|,
x≥3时,f(x)=x+2,f(x)的最大值是f(4)=5,![]() ≤x≤3时,f(x)=3x﹣4,f(x)的最大值是f(3)=5,
≤x≤3时,f(x)=3x﹣4,f(x)的最大值是f(3)=5,
﹣9≤x≤ ![]() 时,f(x)=﹣x﹣2,f(x)的最大值是f(﹣9)=7,
时,f(x)=﹣x﹣2,f(x)的最大值是f(﹣9)=7,
当﹣9≤x≤4时,不等式f(x)<a成立,
则a>7,
即a∈(7,+∞)
【解析】(Ⅰ)通讨论x的范围,得到关于x的不等式组,解出即可;(Ⅱ)通过讨论x的范围,求出各个区间上的f(x)的最大值,求出a的范围即可.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号).

【题目】调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据:出生时间在晚上的男婴为24人,女婴为8人;出生时间在白天的男婴为31人,女婴为26人.
(1)将2×2列联表补充完整.
性别 | 出生时间 | 总计 | |
晚上 | 白天 | ||
男婴 | |||
女婴 | |||
总计 | |||
(2)能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系?
【题目】为分析学生入学时的数学成绩对高一年级数学学习的影响,在高一年级学生中随机抽取10名学生,统计他们入学时的数学成绩和高一期末的数学成绩,如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
入学成绩x(分) | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
高一期末 成绩y(分) | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)求相关系数r;
(2)求y关于x的线性回归方程;
(3)若某学生入学时的数学成绩为80分,试估计他高一期末的数学成绩.
