题目内容
已知函数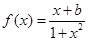 为奇函数。
为奇函数。
(1)判断函数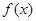 在区间(1,
在区间(1,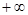 )上的单调性;
)上的单调性;
(2)解关于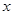 的不等式:
的不等式: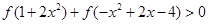 。
。
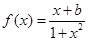 为奇函数。
为奇函数。(1)判断函数
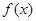 在区间(1,
在区间(1, )上的单调性;
)上的单调性;(2)解关于
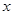 的不等式:
的不等式: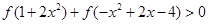 。
。(1)函数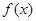 在(1,
在(1,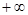 )上是减函数。(2)
)上是减函数。(2)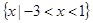
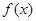 在(1,
在(1,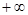 )上是减函数。(2)
)上是减函数。(2)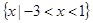
本试题主要是考查了函数的单调性的运用,函数奇偶性的判定,并且运用单调性求解抽象不等式的综合运用。
(1)利用函数的奇函数的性质f(0)=0,得到参数的值,然后判定函数的单调性。
(2)利用函数的单调性,和奇偶性化简表达式为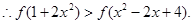 ,然后结合定义域和单调性得到不等式,进而解得。
,然后结合定义域和单调性得到不等式,进而解得。
解:(1)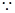 函数
函数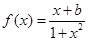 为定义在R上的奇函数,
为定义在R上的奇函数,
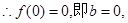
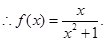 ……………………2分
……………………2分
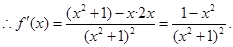 ……………………4分
……………………4分
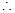 函数
函数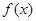 在(1,
在(1,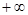 )上是减函数。 …………………6分
)上是减函数。 …………………6分
(2)由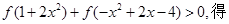
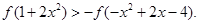
 是奇函数,
是奇函数, 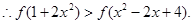 ………………………8分
………………………8分
又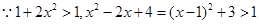 ,且
,且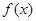 在(1,
在(1,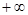 )上为减函数,
)上为减函数,
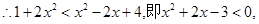 解得
解得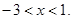
 不等式
不等式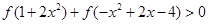 的解集是
的解集是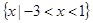
(1)利用函数的奇函数的性质f(0)=0,得到参数的值,然后判定函数的单调性。
(2)利用函数的单调性,和奇偶性化简表达式为
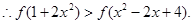 ,然后结合定义域和单调性得到不等式,进而解得。
,然后结合定义域和单调性得到不等式,进而解得。解:(1)
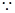 函数
函数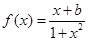 为定义在R上的奇函数,
为定义在R上的奇函数,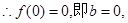
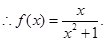 ……………………2分
……………………2分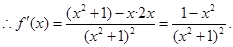 ……………………4分
……………………4分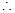 函数
函数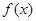 在(1,
在(1,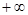 )上是减函数。 …………………6分
)上是减函数。 …………………6分(2)由
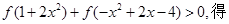
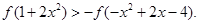
 是奇函数,
是奇函数, 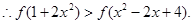 ………………………8分
………………………8分又
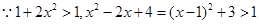 ,且
,且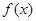 在(1,
在(1,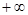 )上为减函数,
)上为减函数,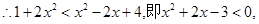 解得
解得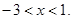
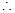 不等式
不等式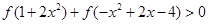 的解集是
的解集是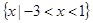

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
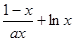 在[1,+∞
在[1,+∞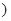 上为增函数.
上为增函数.  的大小,说明理由;
的大小,说明理由; (n∈N*, n≥2)
(n∈N*, n≥2) (
(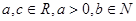 )是奇函数,
)是奇函数, 有最大值
有最大值
 .
.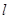 与
与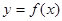 的图象交于P、Q两点,并且使得
的图象交于P、Q两点,并且使得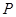 、
、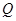 两点关于点
两点关于点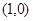 对称,若存在,求出直线
对称,若存在,求出直线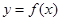 的反函数为
的反函数为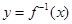 ,定义:若对给定的实数
,定义:若对给定的实数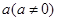 ,函数
,函数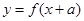 与
与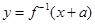 互为反函数,则称
互为反函数,则称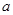 和性质”.
和性质”.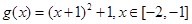 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;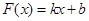 ,其中
,其中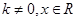 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得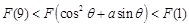 对任意的
对任意的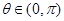 恒成立?若存在,求出
恒成立?若存在,求出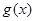 是定义在
是定义在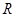 上、以2为周期的函数,若
上、以2为周期的函数,若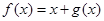 在
在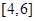 上的值域为
上的值域为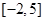 ,则
,则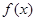 在区间
在区间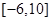 上的值域为 .
上的值域为 .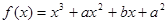 (
(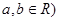
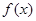 在
在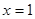 处有极值为
处有极值为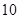 ,求
,求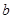 的值;
的值;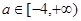 ,
,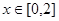 上单调递增,求
上单调递增,求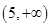 上为增函数,且满足
上为增函数,且满足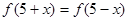 ,则( )
,则( )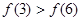
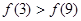
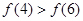
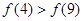
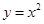
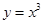
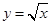
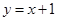
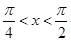 ,则函数
,则函数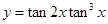 的最大值为 .
的最大值为 .