题目内容

有以下四个命题(n∈N*)：

①n＝n＋1

②2n＞2n＋1(n≥3)

③2＋4＋6＋…＋2n＝n2＋n＋2

④凸n边形对角线的条数

其中满足“假设n＝k(k∈N*，k≥n0)时命题成立，则当n＝k＋1时命题也成立．”但不满足“当n＝n0(n0是题中给定的n的初始值)是命题成立”的命题序号为________．

答案：①③
解析：

　　解析：命题①，当n＝1时不成立，若n＝k时，k＝k＋1，两边同时加1，知k＋1＝(k＋1)＋1，知n＝k＋1时成立，即可以递推．

　　命题②两步均成立．

　　命题③当n＝1时，不成立，但可以递推(可以证明)．事实上，而仅在的基础上增加一个常数2，故不改变递推关系．(即)不变．

　　命题④两步均不成立，事实上由图形知而由知改变了递推关系．

　　点评：该题以数学归纳法原理和步骤为背景，取材于教材反例及习题，是一道“源于教材，高于教材”的好题，要求学生深刻领会数学归纳法的本质即是递推，但奠基验证也必不可少．


练习册系列答案
相关题目
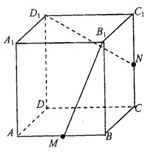16、如图所示，在正方体ABCD-A1B1C1D1中，M、N分别是棱AB、CC1的中点，△MB1P的顶点P在棱CC1与棱C1D1上运动，有以下四个命题：
①平面MB1P⊥ND1；②平面MB1P⊥平面ND1A1；③△MB1P在底面ABCD上的射影图形的面积为定值；④△MB1P在侧面D1C1CD上的射影图形是三角形．
其中正确命题的序号是
②③
．
m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：
①若α∥β，α∥γ，则β∥γ；②若α⊥β，m∥α，则m⊥β；③若m⊥α，m∥β，则α⊥β；
④若y=sin(2x+
π
3
)，则(-
π
12
，0)在函数图象上，其中真命题的序号是（　　）
A、②③B、①④C、①③D、②④
设m、n是不同的直线，α、β是不同的平面，有以下四个命题：
①若m⊥α，n⊥α，则m∥n； 
②若α⊥β，m∥α，则m⊥β；
③若m上α，m⊥n，则n∥α；    
④若n⊥α，n⊥β，则β∥α．
其中，真命题的序号是（　　）
设m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：
①若α∥β，α∥γ，则β∥γ         
②若α⊥β，m∥α，则m⊥β
③若m?α，n⊥β，α∥β，则m⊥n   
④若m∥n，n?α，则m∥α
其中真命题的序号是
①③
①③
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网