题目内容
【题目】已知定义在![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() ,且
,且![]() .
.
(1)求函数![]() ,
,![]() 的解析式;
的解析式;
(2)设函数 ,记
,记![]() (
(![]() ,
,![]() ).探究是否存在正整数
).探究是否存在正整数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 恒成立?若存在,求出所有满足条件的正整数
恒成立?若存在,求出所有满足条件的正整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考结论:设![]() 均为常数,函数
均为常数,函数![]() 的图象关于点
的图象关于点![]() 对称的充要条件是
对称的充要条件是![]() .
.
【答案】(1)![]() ,
,![]() .(2)存在,
.(2)存在,![]() .
.
【解析】
(1)用![]() 替换
替换![]() 后,根据题中奇偶性,利用奇偶性性质得到方程组,即可解得答案。
后,根据题中奇偶性,利用奇偶性性质得到方程组,即可解得答案。
(2)![]() 表达式中分子分母中的自变量格式统一,故可看作是平移后所得,找出其原函数
表达式中分子分母中的自变量格式统一,故可看作是平移后所得,找出其原函数![]() ,根据复合函数奇偶性判断得到
,根据复合函数奇偶性判断得到![]() 的奇偶性,从而得到对称性,再反推得到
的奇偶性,从而得到对称性,再反推得到![]() 的对称情况,利用对称的性质得到函数
的对称情况,利用对称的性质得到函数![]() 的表达式,再利用复合函数单调性判断方法得到
的表达式,再利用复合函数单调性判断方法得到![]() 最小值,借此得到
最小值,借此得到![]() 的取值范围,再根据题目所给条件即可锁定
的取值范围,再根据题目所给条件即可锁定![]() 的取值。
的取值。
解:(1)∵![]() ,
,
∴![]() .
.
又![]() 为偶函数,
为偶函数,![]() 为奇函数,
为奇函数,
∴![]() ,
,![]()
![]() ,
,
∴![]() ,
,![]() .
.
(2)存在满足条件的正整数n.
由题意可知:![]() 为奇函数,其图象关于
为奇函数,其图象关于![]() 中心对称,
中心对称,
∴函数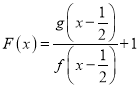 的图象关于点
的图象关于点![]() 中心对称,
中心对称,
即对![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
两式相加,得
![]() ,
,
即![]() .
.
∴![]() .
.
由![]() ,
,
得![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
由此可得![]() 恒成立.
恒成立.
即![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ,且
,且![]() ,
,
则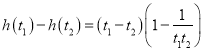
∵![]() ,
,![]() ,∴
,∴![]() .
.
则![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]()
∴![]() .
.
又由已知![]() ,
,![]() ,
,
∴![]()

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目