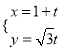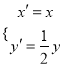题目内容
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的![]() 城市和交通拥堵严重的
城市和交通拥堵严重的![]() 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
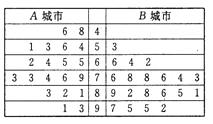
(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求具体解答过程,给出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认同”,请根据此样本完成此列联表,并局此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关;
(Ⅲ)若此样本中的![]() 城市和
城市和![]() 城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自
城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自![]() 城市的概率是多少?
城市的概率是多少?
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
附: 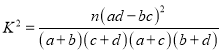
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1) ![]() 城市评分的平均值小于
城市评分的平均值小于![]() 城市评分的平均值;
城市评分的平均值;
![]() 城市评分的方差大于
城市评分的方差大于![]() 城市评分的方差;(2) 没有95%的把握认为城市拥堵与认可共享单车有关;(3)
城市评分的方差;(2) 没有95%的把握认为城市拥堵与认可共享单车有关;(3)![]() .
.
【解析】试题分析:(1)由茎叶图可知, ![]() 城市评分集中数值比
城市评分集中数值比![]() 城市评分数值更大,所以B城市的平均数较大,方差较小。(2)根据所填
城市评分数值更大,所以B城市的平均数较大,方差较小。(2)根据所填![]() 列联表,代入
列联表,代入![]() ,可知没有95%的把握认为城市拥堵与认可共享单车有关。(3)利用条件概率公式可求。
,可知没有95%的把握认为城市拥堵与认可共享单车有关。(3)利用条件概率公式可求。
试题分析:(Ⅰ)由茎叶图可知, ![]() 城市评分集中数值比
城市评分集中数值比![]() 城市评分数值更大,所以
城市评分数值更大,所以![]() 城市评分的平均值小于
城市评分的平均值小于![]() 城市评分的平均值;
城市评分的平均值; ![]() 城市评分的方差大于
城市评分的方差大于![]() 城市评分的方差;
城市评分的方差;
(Ⅱ)
|
| 合计 | |
认可 | 5 | 10 | 15 |
不认可 | 15 | 10 | 25 |
20 | 20 | 40 |
![]()
所以没有95%的把握认为城市拥堵与认可共享单车有关;
(Ⅲ)设事件![]() :恰有一人认可;事件
:恰有一人认可;事件![]() :来自
:来自![]() 城市的人认可;
城市的人认可;
事件![]() 包含的基本事件数为
包含的基本事件数为![]() ,
,
事件![]() 包含的基本事件数为
包含的基本事件数为![]() ,
,
则所求的条件概率![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某高中在校学生2 000人,高一年级与高二年级人数相同并且都比高三年级多1人.为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
年级 项目 | 高一年级 | 高二年级 | 高三年级 |
跑步 | a | b | c |
跳绳 | x | y | z |
其中a∶b∶c=2∶3∶5,全校参与跳绳的人数占总人数的![]() . 为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?
. 为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?