题目内容
下列命题:
①函数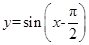 在
在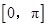 上是减函数;
上是减函数;
②点A(1,1)、B(2,7)在直线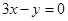 两侧;
两侧;
③数列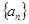 为递减的等差数列,
为递减的等差数列,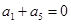 ,设数列
,设数列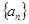 的前n项和为
的前n项和为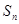 ,则当
,则当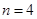 时,
时,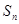 取得最大值;
取得最大值;
④定义运算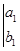
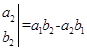 则函数
则函数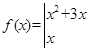
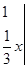 的图象在点
的图象在点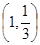 处的切线方程是
处的切线方程是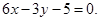 其中正确命题的序号是 (把所有正确命题的序号都写上).
其中正确命题的序号是 (把所有正确命题的序号都写上).
①函数
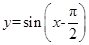 在
在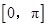 上是减函数;
上是减函数; ②点A(1,1)、B(2,7)在直线
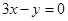 两侧;
两侧; ③数列
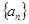 为递减的等差数列,
为递减的等差数列,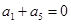 ,设数列
,设数列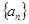 的前n项和为
的前n项和为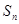 ,则当
,则当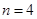 时,
时,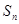 取得最大值;
取得最大值;④定义运算
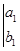
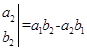 则函数
则函数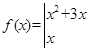
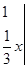 的图象在点
的图象在点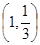 处的切线方程是
处的切线方程是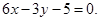 其中正确命题的序号是 (把所有正确命题的序号都写上).
其中正确命题的序号是 (把所有正确命题的序号都写上).②④
对①,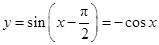 ,从而可知函数
,从而可知函数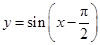 在
在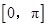 上是增函数,为假命题;对②,由
上是增函数,为假命题;对②,由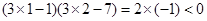 可知,点A(1,1)、B(2,7)在直线
可知,点A(1,1)、B(2,7)在直线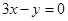 两侧,为真命题;对③,由
两侧,为真命题;对③,由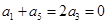 ,得
,得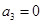 ,又数列
,又数列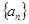 单调递减,所以当
单调递减,所以当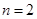 或
或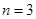 时,
时,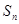 取得最大值,为假命题;
取得最大值,为假命题;
对④,由定义可知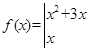
 ,故
,故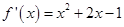 .则
.则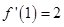 .所以函数
.所以函数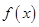 在点
在点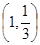 处的切线方程为
处的切线方程为 ,化为一般式为
,化为一般式为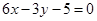 ,为真命题.
,为真命题.
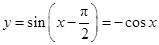 ,从而可知函数
,从而可知函数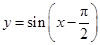 在
在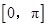 上是增函数,为假命题;对②,由
上是增函数,为假命题;对②,由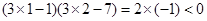 可知,点A(1,1)、B(2,7)在直线
可知,点A(1,1)、B(2,7)在直线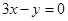 两侧,为真命题;对③,由
两侧,为真命题;对③,由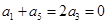 ,得
,得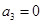 ,又数列
,又数列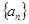 单调递减,所以当
单调递减,所以当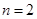 或
或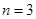 时,
时,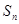 取得最大值,为假命题;
取得最大值,为假命题;对④,由定义可知
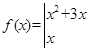
 ,故
,故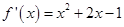 .则
.则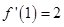 .所以函数
.所以函数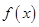 在点
在点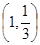 处的切线方程为
处的切线方程为 ,化为一般式为
,化为一般式为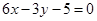 ,为真命题.
,为真命题.
练习册系列答案
相关题目
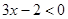 ,则
,则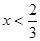 ”的逆否命题为______________________.
”的逆否命题为______________________.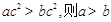 ”的逆命题; ④若“
”的逆命题; ④若“ ,
, ”
” 中,若
中,若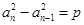 ,(n≥2,n∈N*,p为常数),则称
,(n≥2,n∈N*,p为常数),则称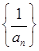 是等差数列;②
是等差数列;②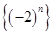 是“等方差数列”;
是“等方差数列”; 为实数,则“
为实数,则“ ”是“
”是“ 的△ABC的个数为2;
的△ABC的个数为2;  的夹角为钝角,则实数
的夹角为钝角,则实数 的取值范围
的取值范围 ;
; 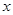 为三角形中的最小内角,则函数
为三角形中的最小内角,则函数 的值域是
的值域是 ;
; 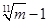 ;
;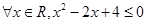 ”的否定为( )
”的否定为( )



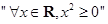 的否定是
的否定是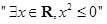 ;
;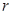 的绝对值越接近于
的绝对值越接近于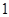 ,表明两个随机变量线性相关性越强;
,表明两个随机变量线性相关性越强;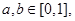 则不等式
则不等式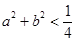 成立的概率是
成立的概率是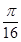 ;
; 中,若cos(2B+C)+2sinAsinB=0则
中,若cos(2B+C)+2sinAsinB=0则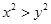 ,则
,则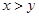 ”的逆否命题是
”的逆否命题是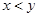 ,则
,则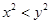 ”
”
 ,则
,则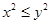 ”
”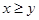 ,则
,则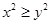 ”
”