题目内容
【题目】已知函数f(x)=|x+m|+|2x﹣1|(m∈R).
(1)当m=﹣1时,求不等式f(x)≤2的解集;
(2)设关于x的不等式f(x)≤|2x+1|的解集为A,且[1,2]A,求实数m的取值范围.
【答案】
(1)解:当m=﹣1时,函数f(x)=|x﹣1|+|2x﹣1|,不等式f(x)≤2,即|x﹣1|+|2x﹣1|≤2,
故有 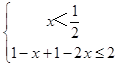 ①,或
①,或 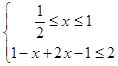 ②,或
②,或 ![]() ③.
③.
解①求得0≤x< ![]() ,解②求得
,解②求得 ![]() ≤x≤1,解③求得1<x≤
≤x≤1,解③求得1<x≤ ![]() .
.
综上可得,不等式f(x)≤2的解集为{x|0≤x≤ ![]() }
}
(2)解:由题意可得,当x∈[1,2]时,关于x的不等式f(x)≤|2x+1|恒成立,
即|x+m|+|2x﹣1|≤|2x+1|恒成立,即|x+m|≤(2x+1)﹣(2x﹣1)=2 恒成立,
∴﹣2≤x+m≤2 恒成立,即﹣x﹣2≤m≤2﹣m 恒成立,∴﹣3≤m≤0,
即实数m的取值范围为[﹣3,0]
【解析】(1)当m=﹣1时,把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(2)由题意可得,当x∈[1,2]时,关于x的不等式f(x)≤|2x+1|恒成立,即﹣2≤x+m≤2 恒成立,即﹣x﹣2≤m≤2﹣m 恒成立,由此可得实数m的取值范围.
【考点精析】利用绝对值不等式的解法对题目进行判断即可得到答案,需要熟知含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案【题目】为了了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x/万元 | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y/万元 | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据上表可得回归直线方程![]() x+
x+![]() ,其中
,其中![]() =0.76,
=0.76, ![]() ,据此估计,该社区一户居民年收入为15万元家庭的年支出为_____万元.
,据此估计,该社区一户居民年收入为15万元家庭的年支出为_____万元.
【题目】“世界睡眠日”定在每年的3月21日,某网站于2017年3月14日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2 000人参加调查,现将数据整理分组后如下表所示.
序号(i) | 分组睡眠时间 | 组中值(mi) | 频数(人数) | 频率(fi) |
1 | [4,5) | 4.5 | 80 | |
2 | [5,6) | 5.5 | 520 | 0.26 |
3 | [6,7) | 6.5 | 600 | 0.30 |
4 | [7,8) | 7.5 | ||
5 | [8,9) | 8.5 | 200 | 0.10 |
6 | [9,10] | 9.5 | 40 | 0.02 |
(1)求出表中空白处的数据,并将表格补充完整.
(2)画出频率分布直方图.
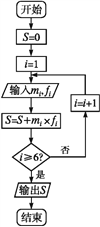
(3)为了对数据进行分析,采用了计算机辅助计算.程序框图如图所示,求输出的S值,并说明S的统计意义.
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下2×2的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式K2= ![]() ,算得K2≈7.61
,算得K2≈7.61
附表:
p(K2≥k0) | 0.025 | 0.01 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确是( )
A.有99.5%以上的把握认为“爱好该项运动与性别有关”
B.有99.5%以上的把握认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”


