题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 经过点
经过点![]() ,其离心率为
,其离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() ,
,![]() 为椭圆
为椭圆![]() 的焦点,且
的焦点,且![]() ,求点
,求点![]() 到
到![]() 轴的距离.
轴的距离.
【答案】(1)![]() (2)
(2) ![]()
【解析】
(1)椭圆E经过点A(4,0),可得 a=4. 椭圆E的离心率e![]() 可得c=2
可得c=2![]() . 即可得椭圆E的方程;
. 即可得椭圆E的方程;
(2)由∠F1PF2![]() ,所以
,所以![]()
![]() 0,可得x2+y2=12,由
0,可得x2+y2=12,由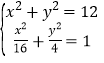 ,得P到y轴的距离.
,得P到y轴的距离.
(1)因为椭圆![]() 经过点
经过点![]() ,
,
所以![]() ,解得
,解得![]() .
.
又椭圆![]() 的离心率
的离心率![]() ,所以
,所以![]() .
.
所以![]() .
.
因此椭圆![]() 的方程为
的方程为![]() .
.
(2)方法一:由椭圆![]() 的方程
的方程![]() ,知
,知![]() ,
,![]() .设
.设![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
由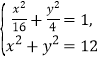 解得
解得![]() .
.
所以![]() ,即
,即![]() 到
到![]() 轴的距离为
轴的距离为![]() .
.
方法二:由椭圆![]() 的方程
的方程![]() ,知
,知![]() .设
.设![]() .
.
因为![]() ,
,![]() 为
为![]() 的中点,
的中点,
所以![]() ,从而
,从而![]() .
.
由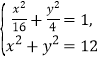 解得
解得![]() .
.
所以![]() ,即
,即![]() 到
到![]() 轴的距离为
轴的距离为![]() .
.
方法三:由椭圆![]() 的方程
的方程![]() ,知
,知![]() ,
,![]()
![]() .设
.设![]() .
.
因为![]() ,所以
,所以![]() .
.
由椭圆的定义可知,![]() ,
,
所以![]() ,
,
所以三角形的面积![]() .
.
又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
代入![]() 得,
得,![]() .
.
所以 ![]() ,即
,即![]() 到
到![]() 轴的距离为
轴的距离为![]() .
.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目