题目内容
(本小题满分12分)在等差数列 中,
中, ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,求
的等比数列,求 的前
的前 项和
项和 .
.
 中,
中, ,
, .
.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)设数列
 是首项为
是首项为 ,公比为
,公比为 的等比数列,求
的等比数列,求 的前
的前 项和
项和 .
.(1)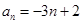
(2) 当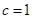 时,
时,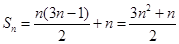 ,当
,当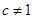 时,
时,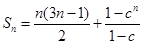 .
.
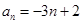
(2) 当
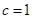 时,
时,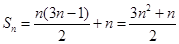 ,当
,当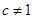 时,
时,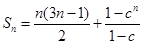 .
.试题分析:(Ⅰ)设等差数列
 的公差是
的公差是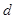 .
.依题意
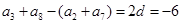 ,从而
,从而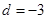 . ………………2分
. ………………2分所以
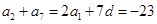 ,解得
,解得 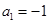 . ………………4分
. ………………4分所以数列
 的通项公式为
的通项公式为 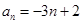 . ………………6分
. ………………6分(Ⅱ)由数列
 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,得
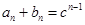 ,即
,即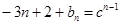 ,
,所以
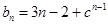 . ………………8分
. ………………8分所以
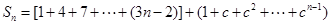
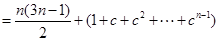 . ………………10分
. ………………10分从而当
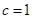 时,
时,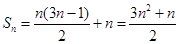 ; ………………11分
; ………………11分当
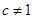 时,
时,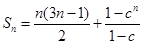 . ………………12分
. ………………12分点评:解决该试题的关键是能结合已知中等差数列的项的关系式,解方程组得到通项公式。同时能利用分组求和法得到和,易错点是对于c是否为1,进行分类讨论,中档题。

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为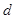 的等差数列;
的等差数列;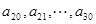 是公差为
是公差为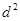 的等差数列(
的等差数列( ).
).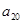 = 30,求
= 30,求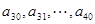 是公差为
是公差为 关于
关于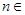 N
N );
); ,试用
,试用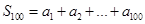

 中,
中,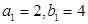 且
且 成等差数列,
成等差数列, 成等比数列
成等比数列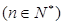
 及
及 ;
;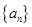 的前
的前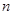 项和为
项和为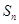 满足:
满足: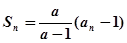 (
(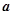 为常数,且
为常数,且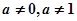 )
) 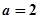 ,求数列
,求数列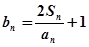 ,若数列
,若数列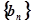 为等比数列,求
为等比数列,求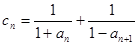 ,数列
,数列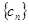 前
前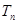 ,求证
,求证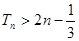
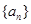 是等差数列,
是等差数列,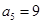 ,
,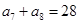 ,则
,则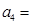
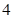
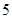
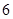
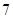
 }的前n项和为
}的前n项和为 ,
, ,则
,则 。
。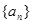 的前
的前 项和为
项和为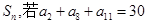 ,那么
,那么 值的是 ( )
值的是 ( )