题目内容
已知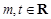 ,函数
,函数 .
.
(Ⅰ)当 时,
时,
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若关于 的不等式
的不等式 在区间
在区间 上有解,求
上有解,求 的取值范围;
的取值范围;
(Ⅱ)已知曲线 在其图象上的两点
在其图象上的两点 ,
, (
( )处的切线分别为
)处的切线分别为 .若直线
.若直线 与
与 平行,试探究点
平行,试探究点 与点
与点 的关系,并证明你的结论.
的关系,并证明你的结论.
(Ⅰ)(1) 单调递增区间为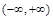 ;(2)
;(2) 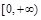 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)(1)根据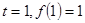 求出
求出 的值,然后利用
的值,然后利用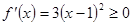 ,得到函数在定义域内都是单调递增的,从而写出其单调区间;
,得到函数在定义域内都是单调递增的,从而写出其单调区间;
(2)当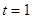 时,将不等式化简,整理为
时,将不等式化简,整理为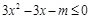 在区间
在区间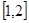 上有解问题,可以反解
上有解问题,可以反解 ,利用不等式
,利用不等式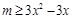 在区间
在区间 上有解,即
上有解,即 大于等于其最小值,转化为求
大于等于其最小值,转化为求 在区间
在区间 上的最小值,
上的最小值,
(Ⅱ)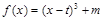 的对称中心为
的对称中心为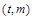 ,故合情猜测,若直线
,故合情猜测,若直线 与
与 平行,则点
平行,则点 与点
与点 关于点
关于点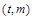 对称.然后对猜测进行证明,首先求其两点处的导数,即两切线的斜率,利用平行及斜率相等,证明
对称.然后对猜测进行证明,首先求其两点处的导数,即两切线的斜率,利用平行及斜率相等,证明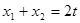 ,
,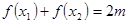 .
.
试题解析:(Ⅰ)(1)因为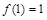 ,所以
,所以 , 1分
, 1分
则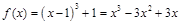 ,
,
而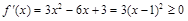 恒成立,
恒成立,
所以函数 的单调递增区间为
的单调递增区间为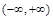 . 4分
. 4分
(2)不等式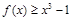 在区间
在区间 上有解,
上有解,
即不等式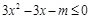 在区间
在区间 上有解,
上有解,
即不等式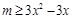 在区间
在区间 上有解,
上有解,
等价于 不小于
不小于 在区间
在区间 上的最小值. 6分
上的最小值. 6分
因为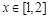 时,
时,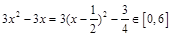 ,
,
所以 的取值范围是
的取值范围是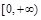 . 9分
. 9分
Ⅱ.因为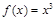 的对称中心为
的对称中心为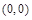 ,
,
而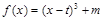 可以由
可以由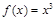 经平移得到,
经平移得到,
所以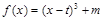 的对称中心为
的对称中心为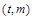 ,故合情猜测,若直线
,故合情猜测,若直线 与
与 平行,
平行,
则点 与点
与点 关于点
关于点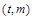 对称. 10分
对称. 10分
对猜想证明如下:
因为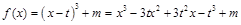 ,
,
所以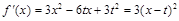 ,
,
所以 ,
, 的斜率分别为
的斜率分别为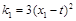 ,
,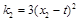 .
.
又直线 与
与 平行,所以
平行,所以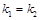 ,即
,即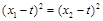 ,
,
因为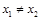 ,所以,
,所以,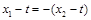 , 12分
, 12分
从而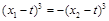 ,
,
所以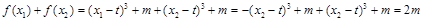

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
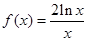
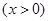
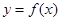 在
在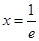 处的切线的斜率;
处的切线的斜率;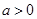 ,求函数
,求函数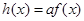 在
在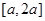 上的最大值.
上的最大值. 的图象在点
的图象在点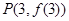 处的切线方程为
处的切线方程为 .
. 的值;
的值; .
. 是
是 上的增函数,求实数
上的增函数,求实数 的最大值;
的最大值; ,使得过点
,使得过点 围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点
围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点 ,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).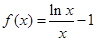 .
. 的单调性;
的单调性;  ,求
,求 上的最大值;
上的最大值; ,不等式
,不等式 都成立(其中
都成立(其中 是自然对数的底数).
是自然对数的底数). ,
, .
. ,讨论
,讨论 在
在 内的单调性并求极值;
内的单调性并求极值; 时,恒有
时,恒有 .
. ,
, .
. ,使得
,使得 ,求a的取值范围;
,求a的取值范围; 有两个不同的实数解
有两个不同的实数解 ,证明:
,证明: .
.
 .
.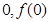 )处的切线方程;
)处的切线方程; 使得
使得 ,求
,求 的取值范围.
的取值范围.