题目内容
设函数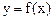 是定义在
是定义在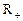 上的函数,并且满足下面三个条件:(1)对正数x、y都有
上的函数,并且满足下面三个条件:(1)对正数x、y都有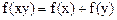 ;(2)当
;(2)当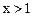 时,
时,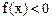 ;(3)
;(3)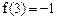 。则
。则
(Ⅰ)求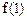 和
和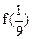 的值;
的值;
(Ⅱ)如果不等式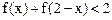 成立,求x的取值范围.
成立,求x的取值范围.
(Ⅲ)如果存在正数k,使不等式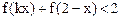 有解,求正数
有解,求正数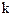 的取值范围.
的取值范围.
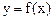 是定义在
是定义在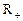 上的函数,并且满足下面三个条件:(1)对正数x、y都有
上的函数,并且满足下面三个条件:(1)对正数x、y都有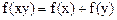 ;(2)当
;(2)当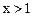 时,
时,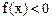 ;(3)
;(3)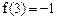 。则
。则(Ⅰ)求
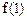 和
和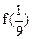 的值;
的值;(Ⅱ)如果不等式
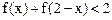 成立,求x的取值范围.
成立,求x的取值范围.(Ⅲ)如果存在正数k,使不等式
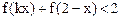 有解,求正数
有解,求正数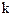 的取值范围.
的取值范围.(1)2;(2)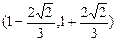 ;(3)
;(3)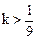 。
。
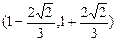 ;(3)
;(3)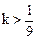 。
。解:(Ⅰ)令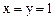 易得
易得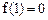 .而
.而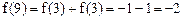
且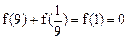 ,得
,得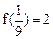 .
.
(Ⅱ)设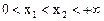 ,由条件(1)可得
,由条件(1)可得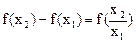 ,因
,因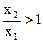 ,由(2)知
,由(2)知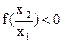 ,所以
,所以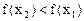 ,即
,即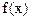 在
在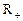 上是递减的函数.
上是递减的函数.
由条件(1)及(Ⅰ)的结果得: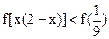 其中
其中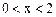 ,由函数
,由函数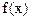 在
在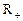 上的递减性,可得:
上的递减性,可得: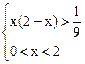 ,由此解得x的范围是
,由此解得x的范围是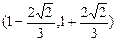 .
.
(Ⅲ)同上理,不等式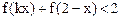 可化为
可化为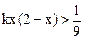 且
且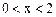 ,
,
得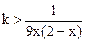 ,此不等式有解,等价于
,此不等式有解,等价于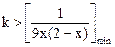 ,在
,在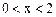 的范围内,易知
的范围内,易知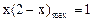 ,故
,故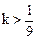 即为所求范围.
即为所求范围.
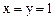 易得
易得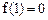 .而
.而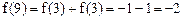
且
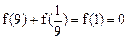 ,得
,得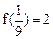 .
.(Ⅱ)设
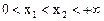 ,由条件(1)可得
,由条件(1)可得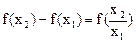 ,因
,因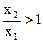 ,由(2)知
,由(2)知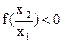 ,所以
,所以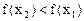 ,即
,即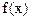 在
在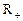 上是递减的函数.
上是递减的函数.由条件(1)及(Ⅰ)的结果得:
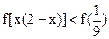 其中
其中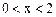 ,由函数
,由函数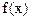 在
在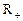 上的递减性,可得:
上的递减性,可得: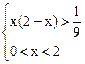 ,由此解得x的范围是
,由此解得x的范围是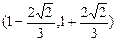 .
.(Ⅲ)同上理,不等式
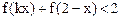 可化为
可化为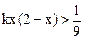 且
且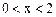 ,
,得
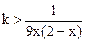 ,此不等式有解,等价于
,此不等式有解,等价于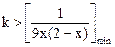 ,在
,在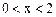 的范围内,易知
的范围内,易知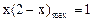 ,故
,故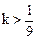 即为所求范围.
即为所求范围.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
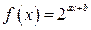 在[1,2]上的最小值为1,最大值为2,求
在[1,2]上的最小值为1,最大值为2,求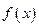 的解析式.
的解析式.
 的单调区间
的单调区间 都有
都有 成立,求实数a的取值范围
成立,求实数a的取值范围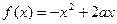 与
与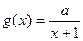 在区间
在区间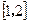 上都是减函数,则a的取值范围是( )
上都是减函数,则a的取值范围是( )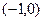
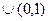 B
B 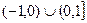 C
C 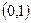 D
D 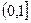
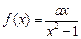 (
(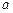 ≠0)在区间(-1,1)上的单调性。
≠0)在区间(-1,1)上的单调性。 ,都有
,都有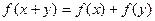 ,且
,且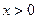 时,f(x)<0,f(1)=-2.
时,f(x)<0,f(1)=-2.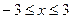 时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.
时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.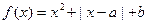 在区间
在区间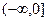 上为减函数,则实数
上为减函数,则实数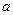 的取值范围是( )
的取值范围是( )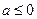 ;
;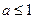 ;
;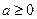 ;
;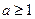
 满足:对任意实数
满足:对任意实数 ,当
,当 时,总有
时,总有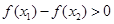 ,那么实数
,那么实数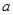 的取值范围是( )
的取值范围是( )


