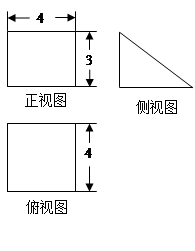
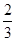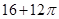题目内容
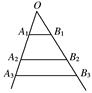
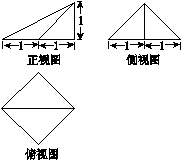
如图是某三棱柱被削去一个底面后的直观图、侧(左)视图与俯视图．已知CF＝2AD，侧视图是边长为2的等边三角形，俯视图是直角梯形，有关数据如图所示．求该几何体的体积．
3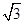
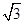
解：取CF中点P，过P作PQ∥CB交BE于Q，连接PD，QD，则AD∥CP，且AD＝CP.
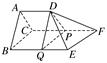
所以四边形ACPD为平行四边形，
所以AC∥PD.
所以平面PDQ∥平面ABC.
该几何体可分割成三棱柱PDQ－CAB和四棱锥D－PQEF，
所以V＝VPDQ－CAB＋VD－PQEF
＝
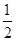×22sin 60°×2＋
×
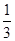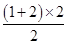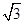×＝3.
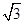所以四边形ACPD为平行四边形，
所以AC∥PD.
所以平面PDQ∥平面ABC.
该几何体可分割成三棱柱PDQ－CAB和四棱锥D－PQEF，
所以V＝VPDQ－CAB＋VD－PQEF
＝
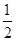×22sin 60°×2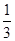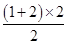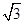＋××＝3.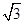
练习册系列答案
阅读快车系列答案
相关题目
BB'=CC'=AB,则多面体ABC-A'B'C'的正视图是( )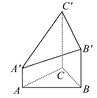 
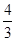πr3，观察发现V′＝S.则由四维空间中“超球”的三维测度V＝8πr3，猜想其四维测度W＝________.
