题目内容

5．已知数列{an}中，a1=0，an+1=an+2n-1．
（1）写出此数列的前四项；
（2）根据前四项，猜出数列的一个通项公式．

分析 （1）由a1=0，an+1=an+2n-1．分别取n=1，2，3．即可得出．
（2）由（1）可得：a1=（1-1）2，a2=（2-1）2，a3=（3-1）2，a4（4-1）2．即可出猜想：an．

解答 解：（1）∵a1=0，an+1=an+2n-1．∴a2=a1+1=1，a3=a2+3=4，a4=a3+5=9．
（2）由（1）可得：a1=0=（1-1）2，a2=1=（2-1）2，a3=4=（3-1）2，a4=9=（4-1）2．
猜想：an=（n=1）2．

点评 本题考查了递推关系的应用，考查了猜想归纳推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
15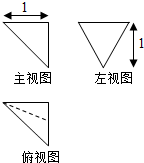．一个三棱锥的三视图如图所示，主视图和俯视图为全等的等腰直角三角形，则该三棱锥的体积为（　　）
A．$\frac{1}{12}$B．$\frac{1}{6}$C．$\frac{1}{4}$D．$\frac{1}{3}$
16．已知函数f（x）=x3+ax2+x+2（a＞0）的极大值点和极小值点都在区间（-1，1）内，则实数a的取值范围是（$\sqrt{3}$，2）．
13．Rt△ABC中，∠C=90°，AC=BC=2，⊙C的半径是1，MN是⊙C直径，求：$\overrightarrow{AM}$•$\overrightarrow{BN}$的最大值及此时$\overrightarrow{MN}$与$\overrightarrow{AB}$的关系．
20．在数列{an}中，a1=0，an+1+Sn=n2+2n（n∈N*），则数列{an}的通项公式是${a}_{n}=\left\{\begin{array}{l}{0，n=1}\\{2n-1，n≥2}\end{array}\right.$．
10．下列命题中正确的是②③． （填序号）
①命题“对任意x∈R，有x2≥0”的否定是“存在x0∈R，有x02≥0”．
②命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1，则x2-3x+2≠0”．
③指数函数是增函数，f（x）=2-x是指数函数，因此f（x）=2-x是增函数．以上推理过程中大前提不正确．
④若a，b，c∈R，则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0”．
17．已知数列{an}满足an+1=2an+1，且首项a1=1，那么a4的值是（　　）
A．7B．14C．15D．8
14．已知a=cos（-2037°），b=cos852°，则a、b的大小关系为（　　）
A．a=bB．a＞bC．a＜bD．无法确定
15．（1）化简：$\frac{sin（π-α）cos（3π-α）tan（-α-π）tan（α-2π）}{tan（4π-α）sin（5π+α）}$
（2）已知tanα=3，计算  $\frac{4sinα-2cosα}{5cosα+3sinα}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网