题目内容
13. Rt△ABC中,∠C=90°,AC=BC=2,⊙C的半径是1,MN是⊙C直径,求:$\overrightarrow{AM}$•$\overrightarrow{BN}$的最大值及此时$\overrightarrow{MN}$与$\overrightarrow{AB}$的关系.
Rt△ABC中,∠C=90°,AC=BC=2,⊙C的半径是1,MN是⊙C直径,求:$\overrightarrow{AM}$•$\overrightarrow{BN}$的最大值及此时$\overrightarrow{MN}$与$\overrightarrow{AB}$的关系.
分析 如图所示,建立直角坐标系.则A$(-\sqrt{2},-\sqrt{2})$,B$(\sqrt{2},-\sqrt{2})$.设M(cosθ,sinθ),N(-cosθ,-sinθ)(θ∈[0,2π)).可得$\overrightarrow{AM}$•$\overrightarrow{BN}$=-$2\sqrt{2}$cosθ-1≤2$\sqrt{2}$-1,当且仅当θ=π时取等号.即可得出.
解答 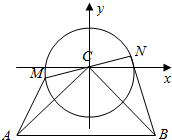 解:如图所示,建立直角坐标系.
解:如图所示,建立直角坐标系.
则A$(-\sqrt{2},-\sqrt{2})$,B$(\sqrt{2},-\sqrt{2})$.
设M(cosθ,sinθ),N(-cosθ,-sinθ)(θ∈[0,2π)).
$\overrightarrow{AM}$=(cosθ+$\sqrt{2}$,sinθ$+\sqrt{2}$),$\overrightarrow{BN}$=(-cosθ-$\sqrt{2}$,-sinθ+$\sqrt{2}$).
∴$\overrightarrow{AM}$•$\overrightarrow{BN}$=-2$\sqrt{2}$cosθ-1≤2$\sqrt{2}$-1,
当且仅当θ=π时取等号.
此时$\overrightarrow{AB}$=$(2\sqrt{2},0)$,$\overrightarrow{MN}$=(2,0).
∴$\overrightarrow{AB}$=$\sqrt{2}$$\overrightarrow{MN}$,共线.
点评 本题考查了向量的坐标运算、数量积运算性质、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.数列{an}满足an+1+(-1)nan=2n-1,则{an}的前80项和为( )
| A. | 3690 | B. | 3660 | C. | 3240 | D. | 1830 |
8.在△ABC中,若2bccosBcosC=b2sin2C+c2sin2B,那么△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
2.已知函数f(x)=log${\;}_{\frac{1}{2}}$x,x∈[$\frac{1}{4}$,$\frac{\sqrt{2}}{2}$],则f(x)的值域是( )
| A. | [$\frac{1}{2}$,2] | B. | [-$\frac{1}{2}$,2] | C. | [0,2] | D. | [0,$\frac{1}{2}$] |
3.某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
B配方的频数分布表
(1)分别估计用A配方,B配方生产的产品的优质品率;
(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y=$\left\{\begin{array}{l}{-2,t<94}\\{2,94≤t<102}\\{4,t≥102}\end{array}\right.$
估计用B配方生产的一件产品的利润大于0的概率,并求用B配方生产的上述100件产品平均一件的利润.
A配方的频数分布表
| 指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
| 频数 | 8 | 20 | 42 | 22 | 8 |
| 指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
| 频数 | 4 | 12 | 42 | 32 | 10 |
(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y=$\left\{\begin{array}{l}{-2,t<94}\\{2,94≤t<102}\\{4,t≥102}\end{array}\right.$
估计用B配方生产的一件产品的利润大于0的概率,并求用B配方生产的上述100件产品平均一件的利润.
