题目内容
1．若关于x的一元二次实系数方程x2+px+q=0有一个根为 1+i，（i为虚数单位），则p+q的值是0．分析 关于x的一元二次实系数方程x2+px+q=0有一个根为 1+i，（i为虚数单位），则1-i也是次方程的一个虚根，利用根与系数的关系即可得出．
解答 解：关于x的一元二次实系数方程x2+px+q=0有一个根为 1+i，（i为虚数单位），
则1-i也是次方程的一个虚根，
∴$\left\{\begin{array}{l}{（1+i）+（1-i）=-p}\\{（1+i）（1-i）=q}\end{array}\right.$，解得p=-2，q=2．
∴p+q=0．
故答案为：0．
点评 本题考查了实系数一元二次方程的虚根成对原理、根与系数的关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
16．从一群游戏的孩子中随机抽出k人，每人分一个苹果，让他们返回继续游戏．过一会儿，再从中任取m人，发现其中有n个孩子曾分过苹果，估计参加游戏的孩子的人数为（ ）
| A． | $\frac{kn}{m}$ | B． | $\frac{km}{n}$ | C． | k+m-n | D． | k+m+n |
6．
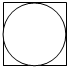在如图的正方形中随机撒一把豆子，用随机模拟的方法估圆周率的值：经查数，落在正方形中的豆子的总数为n粒，其中m（m＜n）粒豆子落在该正方形的内切圆内，以此估计圆周率π为（ ）
在如图的正方形中随机撒一把豆子，用随机模拟的方法估圆周率的值：经查数，落在正方形中的豆子的总数为n粒，其中m（m＜n）粒豆子落在该正方形的内切圆内，以此估计圆周率π为（ ）| A． | $\frac{m}{n}$ | B． | $\frac{2m}{n}$ | C． | $\frac{3m}{n}$ | D． | $\frac{4m}{n}$ |
10．关于z的方程z+i=2+iz的根是（ ）
| A． | $\frac{3}{2}-\frac{1}{2}$i | B． | $\frac{3}{2}+\frac{1}{2}$i | C． | 3-i | D． | 3+i |