题目内容
11.已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积、体积.分析 如图所示,由等边三角形的面积计算公式可得:△SAB的面积=$\frac{\sqrt{3}}{4}{a}^{2}$.即可得出四面体S-ABC的表面积.设O为△ABC的中心,延长AO交BC于点D,连接SO,SD,则SO⊥底面ABC,D为BC的中点.可得$AD=\frac{\sqrt{3}}{2}$a=SD,OD=$\frac{1}{3}AD$,AO=$\sqrt{S{D}^{2}-O{D}^{2}}$.利用VS-ABC=$\frac{1}{3}•{S}_{△ABC}×SO$即可得出.
解答 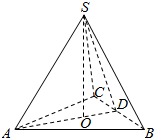 解:如图所示,
解:如图所示,
由等边三角形的面积计算公式可得:△SAB的面积=$\frac{\sqrt{3}}{4}{a}^{2}$.
∴四面体S-ABC的表面积为4×$\frac{\sqrt{3}}{4}{a}^{2}$=$\sqrt{3}{a}^{2}$.
设O为△ABC的中心,延长AO交BC于点D,连接SO,SD,则SO⊥底面ABC,D为BC的中点.
∴$AD=\frac{\sqrt{3}}{2}$a=SD,OD=$\frac{1}{3}AD$=$\frac{\sqrt{3}}{6}$a,
∴AO=$\sqrt{S{D}^{2}-O{D}^{2}}$=$\frac{\sqrt{6}}{3}$a.
∴VS-ABC=$\frac{1}{3}•{S}_{△ABC}×SO$=$\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}$×$\frac{\sqrt{6}}{3}$a=$\frac{\sqrt{2}}{12}{a}^{3}$.
点评 本题考查了等边三角形的性质及其面积计算公式、正三棱锥的性质、线面垂直的判定与性质定理、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

| A. | -i | B. | i | C. | $\frac{3}{5}$-$\frac{4}{5}$i | D. | $\frac{3}{5}$+$\frac{4}{5}$i |

| A. | ①⑥ | B. | ④⑤ | C. | ③④ | D. | ④⑥ |
| A. | 若“p或q”为真命题,则p,q均为真命题 | |
| B. | 命题“若x≥4且y≥2,则x+y≥6”的逆否命题为“若x+y<6,则x<4且y<2” | |
| C. | 若x≠300°,则cosx≠$\frac{1}{2}$ | |
| D. | 命题“?x0∈R,${e}^{{x}_{0}}$≤0”是假命题 |
| A. | a<b<c | B. | a<c<b | C. | a>c>b | D. | a>b>c |