题目内容
已知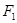 ,
,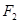 分别是椭圆
分别是椭圆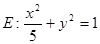 的左、右焦点
的左、右焦点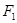 ,
,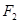 关于直线
关于直线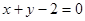 的对称点是圆
的对称点是圆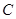 的一条直径的两个端点。
的一条直径的两个端点。
(Ⅰ)求圆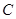 的方程;
的方程;
(Ⅱ)设过点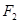 的直线
的直线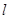 被椭圆
被椭圆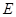 和圆
和圆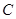 所截得的弦长分别为
所截得的弦长分别为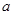 ,
,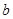 。当
。当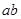 最大时,求直线
最大时,求直线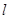 的方程。
的方程。
(Ⅰ)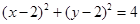 (Ⅱ)
(Ⅱ)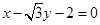 或
或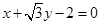
解析

练习册系列答案
相关题目
题目内容
已知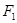 ,
,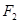 分别是椭圆
分别是椭圆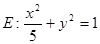 的左、右焦点
的左、右焦点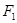 ,
,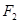 关于直线
关于直线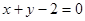 的对称点是圆
的对称点是圆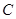 的一条直径的两个端点。
的一条直径的两个端点。
(Ⅰ)求圆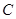 的方程;
的方程;
(Ⅱ)设过点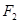 的直线
的直线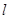 被椭圆
被椭圆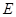 和圆
和圆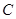 所截得的弦长分别为
所截得的弦长分别为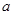 ,
,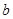 。当
。当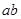 最大时,求直线
最大时,求直线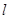 的方程。
的方程。
(Ⅰ)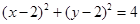 (Ⅱ)
(Ⅱ)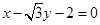 或
或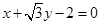
解析
