题目内容
已知数列 的首项
的首项 其中
其中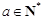 ,
, 令集合
令集合 .
.
(Ⅰ)若 是数列
是数列 中首次为1的项,请写出所有这样数列的前三项;
中首次为1的项,请写出所有这样数列的前三项;
(Ⅱ)求证: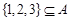 ;
;
(Ⅲ)当 时,求集合
时,求集合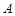 中元素个数
中元素个数 的最大值.
的最大值.
 的首项
的首项 其中
其中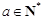 ,
, 令集合
令集合 .
.(Ⅰ)若
 是数列
是数列 中首次为1的项,请写出所有这样数列的前三项;
中首次为1的项,请写出所有这样数列的前三项;(Ⅱ)求证:
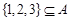 ;
;(Ⅲ)当
 时,求集合
时,求集合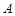 中元素个数
中元素个数 的最大值.
的最大值.(Ⅰ)27,9,3;8,9,3;6,2,3..(Ⅱ)见解析. (Ⅲ)集合 重元素个数
重元素个数 的最大值为21.
的最大值为21.
 重元素个数
重元素个数 的最大值为21.
的最大值为21.试题分析:(Ⅰ)依次代入写出27,9,3;8,9,3;6,2,3.
(Ⅱ)根据
 及
及 须讨论
须讨论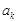 被3除余1,,
被3除余1,,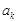 被3除余2,
被3除余2,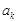 被3除余0,等三种情况.
被3除余0,等三种情况.(Ⅲ)注意由已知递推关系推得数列
 满足:
满足:当
 时,总有
时,总有 成立,其中
成立,其中 .
.因此应注意讨论当
 时,数列
时,数列 中大于3的各项:
中大于3的各项:按逆序排列各项,构成的数列记为
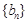 ,由(Ⅰ)可得
,由(Ⅰ)可得 或9,
或9,由(Ⅱ)的证明过程即可知数列
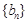 的项满足:
的项满足: ,且当
,且当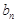 是3的倍数时,若使
是3的倍数时,若使 最小,需使
最小,需使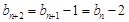 ,
,满足
 最小的数列
最小的数列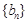 中,
中, 或7,且
或7,且 ,
,得到数列
 是首项为
是首项为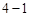 或
或 的公比为3的等比数列,应用等比数列的通项公式即可得出结论.
的公比为3的等比数列,应用等比数列的通项公式即可得出结论.解答本题的关键是注意“转化”成等比数列问题.
试题解析:(Ⅰ)27,9,3;8,9,3;6,2,3. 3分
(Ⅱ)若
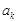 被3除余1,则由已知可得
被3除余1,则由已知可得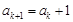 ,
,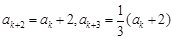 ;
;若
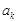 被3除余2,则由已知可得
被3除余2,则由已知可得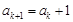 ,
,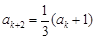 ,
, ;
;若
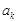 被3除余0,则由已知可得
被3除余0,则由已知可得 ,
, ;
;所以
 ,
,所以
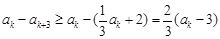
所以,对于数列
 中的任意一项
中的任意一项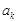 ,“若
,“若 ,则
,则 ”.
”.因为
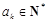 ,所以
,所以 .
.所以数列
 中必存在某一项
中必存在某一项 (否则会与上述结论矛盾!)
(否则会与上述结论矛盾!)若
 ,则
,则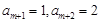 ;若
;若 ,则
,则 ,若
,若 ,则
,则 ,
,由递推关系易得
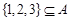 . 8分
. 8分(Ⅲ)集合
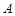 中元素个数
中元素个数 的最大值为21.
的最大值为21.由已知递推关系可推得数列
 满足:
满足:当
 时,总有
时,总有 成立,其中
成立,其中 .
.下面考虑当
 时,数列
时,数列 中大于3的各项:
中大于3的各项:按逆序排列各项,构成的数列记为
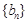 ,由(I)可得
,由(I)可得 或9,
或9,由(Ⅱ)的证明过程可知数列
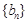 的项满足:
的项满足: ,且当
,且当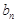 是3的倍数时,若使
是3的倍数时,若使 最小,需使
最小,需使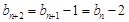 ,
,所以,满足
 最小的数列
最小的数列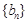 中,
中, 或7,且
或7,且 ,
,所以
 ,所以数列
,所以数列 是首项为
是首项为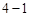 或
或 的公比为3的等比数列,
的公比为3的等比数列,所以
 或
或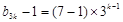 ,即
,即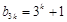 或
或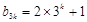 ,
,因为
 ,所以,当
,所以,当 时,
时, 的最大值是6,
的最大值是6,所以
 ,所以集合
,所以集合 重元素个数
重元素个数 的最大值为21. 13分
的最大值为21. 13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
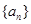 满足
满足
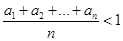 .
. 中,
中, ,
, ,则满足
,则满足 的最大正整数
的最大正整数 的值为 .
的值为 . 满足公比
满足公比 ,
, ,且{
,且{ }中的任意两项之积也是该数列中的一项,若
}中的任意两项之积也是该数列中的一项,若 ,则
,则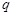 的所有可能取值的集合为 .
的所有可能取值的集合为 .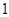 ,公比为
,公比为 的等比数列
的等比数列 的前
的前 项和为
项和为 ,则( )
,则( )


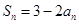
 中,
中, ,
,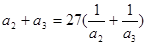 ,则
,则 的通项公式
的通项公式 .
. 的前项n和为
的前项n和为 ,且
,且 ,则
,则 .
.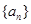 的首项为1,数列
的首项为1,数列 为等比数列且
为等比数列且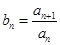 ,若
,若 ,则
,则 ( )
( )