题目内容
(本小题满分12分) 设函数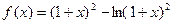
(1)求函数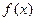 的单调区间;
的单调区间;
(2)若当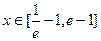 时,不等式
时,不等式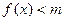 恒成立,求实数
恒成立,求实数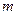 的取值范围;
的取值范围;
(3)若关于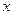 的方程
的方程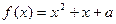 在区间
在区间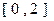 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数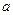 的取值范围。
的取值范围。
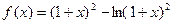
(1)求函数
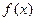 的单调区间;
的单调区间;(2)若当
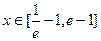 时,不等式
时,不等式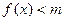 恒成立,求实数
恒成立,求实数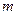 的取值范围;
的取值范围; (3)若关于
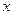 的方程
的方程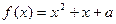 在区间
在区间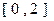 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数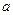 的取值范围。
的取值范围。(1)f(x)的单调增区间为(-2,-1)和(0,+∞),单调减区间(-1,0)和(-∞,-2)(2)m>e2-2(3)2-ln4<a≤3-ln9
因为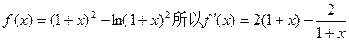
(1)令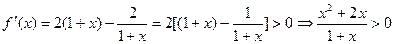
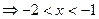 或x>0,所以f(x)的单调增区间为(-2,-1)和(0,+∞);…(3分)
或x>0,所以f(x)的单调增区间为(-2,-1)和(0,+∞);…(3分)
令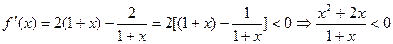
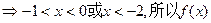 的单调减区间(-1,0)和(-∞,-2)。……(4分)
的单调减区间(-1,0)和(-∞,-2)。……(4分)
(2)令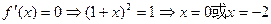 (舍),由(1)知,f(x)连续,
(舍),由(1)知,f(x)连续,
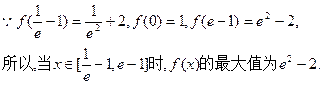

因此可得:f(x)<m恒成立时,m>e2-2 (8分)
(3)原题可转化为:方程a=(1+x)-ln(1+x)2在区间[0,2]上恰好有两个相异的实根。
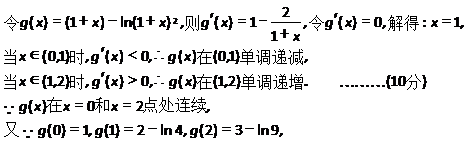

且2-ln4<3-ln9<1,∴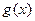 的最大值是1,
的最大值是1,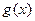 的最小值是2-ln4。
的最小值是2-ln4。
所以在区间[0,2]上原方程恰有两个相异的实根时实数a的取值范围是:
2-ln4<a≤3-ln9 ………………… (12分)
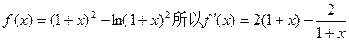
(1)令
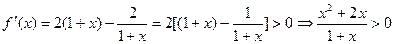
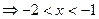 或x>0,所以f(x)的单调增区间为(-2,-1)和(0,+∞);…(3分)
或x>0,所以f(x)的单调增区间为(-2,-1)和(0,+∞);…(3分)令
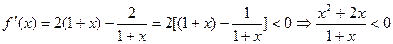
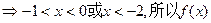 的单调减区间(-1,0)和(-∞,-2)。……(4分)
的单调减区间(-1,0)和(-∞,-2)。……(4分)(2)令
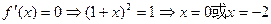 (舍),由(1)知,f(x)连续,
(舍),由(1)知,f(x)连续,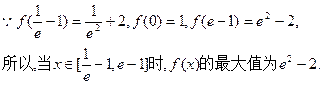

因此可得:f(x)<m恒成立时,m>e2-2 (8分)
(3)原题可转化为:方程a=(1+x)-ln(1+x)2在区间[0,2]上恰好有两个相异的实根。
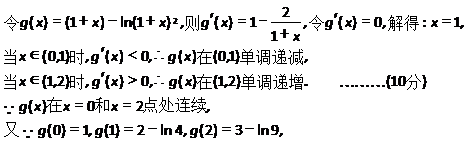

且2-ln4<3-ln9<1,∴
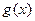 的最大值是1,
的最大值是1,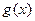 的最小值是2-ln4。
的最小值是2-ln4。所以在区间[0,2]上原方程恰有两个相异的实根时实数a的取值范围是:
2-ln4<a≤3-ln9 ………………… (12分)

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
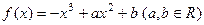 .
.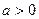 时,求函数
时,求函数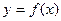 的极值;
的极值;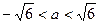 ;
;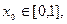
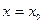 处的切线的斜率为
处的切线的斜率为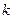 ,求证:
,求证: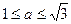 是
是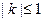 成立的充要条件.
成立的充要条件.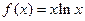 .(Ⅰ)求
.(Ⅰ)求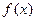 的最小值;
的最小值;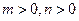 时,求证:
时,求证: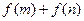 ≥
≥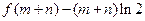 .
.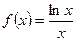 .
.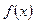 的单调性;
的单调性;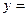
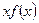 +
+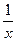 的图像总在直线
的图像总在直线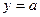 的上方,求实数
的上方,求实数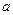 的取值范围;
的取值范围;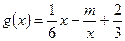 的图像有公共点,且在公共点处的切线相同,求实数
的图像有公共点,且在公共点处的切线相同,求实数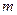 的值.
的值.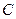 与产量
与产量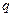 的函数关系式为
的函数关系式为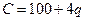
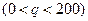 ,价格
,价格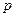 与产量
与产量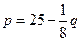 ,求产量
,求产量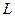 最大。
最大。 ,则实数a取值范围是( )
,则实数a取值范围是( )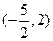
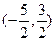
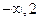 )
)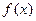 ,有下述四个命题,其中正确命题为( )
,有下述四个命题,其中正确命题为( )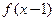 的图象关于点A(1,0)对称;
的图象关于点A(1,0)对称; 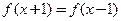 ,则
,则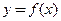 的图象关于直线
的图象关于直线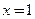 对称;
对称; 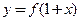 为偶函数,则
为偶函数,则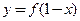 的图象关于直线
的图象关于直线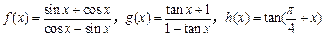 ,下列是同一函数的是( )
,下列是同一函数的是( ) 与
与