题目内容
【题目】已知抛物线![]() 经过点
经过点![]() .
.
(1)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(2)过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,设
两点,设![]() 为原点.
为原点.
(ⅰ)当直线![]() 的斜率为1时,求
的斜率为1时,求![]() 的面积;
的面积;
(ⅱ)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ,
,![]() ;(2)(ⅰ)
;(2)(ⅰ)![]() ;(ⅱ)
;(ⅱ)![]() .
.
【解析】
(1)将点![]() 代入抛物线方程可求得
代入抛物线方程可求得![]() ,进而得到结果;
,进而得到结果;
(2)设![]() ,
,![]()
(i)设直线![]() ,与抛物线方程联立得到韦达定理的形式;由
,与抛物线方程联立得到韦达定理的形式;由![]() ,整理得到
,整理得到![]() ,代入韦达定理可求得结果;
,代入韦达定理可求得结果;
(ii)设直线![]() ,与抛物线方程联立得到韦达定理的形式;由
,与抛物线方程联立得到韦达定理的形式;由![]() ,结合抛物线定义得到
,结合抛物线定义得到![]() ,与韦达定理的结论联立后可求得
,与韦达定理的结论联立后可求得![]() ,进而得到结果.
,进而得到结果.
(1)![]() 抛物线
抛物线![]() 过点
过点![]()
![]() ,解得:
,解得:![]()
![]() 抛物线的方程为
抛物线的方程为![]() ,准线方程为
,准线方程为![]()
(2)由(1)知:![]()
设![]() ,
,![]()
(i)由题意得:直线![]() 的方程为
的方程为![]()
联立 得:
得:![]()

![]() ,
,![]()
![]()
![]()
![]() 的面积为
的面积为![]() .
.
(ii)易知直线![]() 的斜率存在且不为
的斜率存在且不为![]()
设直线![]()
联立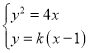 得:
得:![]()

![]()
![]() ,即
,即![]() …③
…③
联立②③,解得: ,代入①得:
,代入①得:![]()
![]()
![]() 直线
直线![]() 的方程为
的方程为![]()

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目