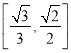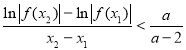题目内容
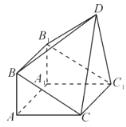
【题目】在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC的中点.将△ABD沿BD折起,使AB⊥AC,连接AE,AC,DE,得到三棱锥A-BCD.
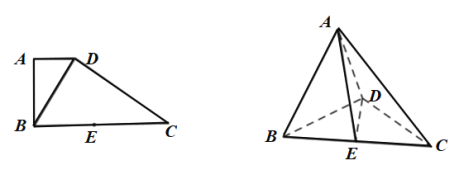
(1)求证:平面ABD⊥平面BCD
(2)若AD=1,二面角C-AB-D的余弦值为![]() ,求二面角B-AD-E的正弦值.
,求二面角B-AD-E的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由AB⊥AC和AB⊥AD,可得AB⊥平面ADC,所以AB⊥CD,而BD⊥DC,所以CD⊥平面ADB,从而可证得平面ABD⊥平面BCD;
(2)由AB⊥平面ADC,可知二面角C-AB-D的平面角为∠CAD,由二面角C-AB-D的余弦值为![]() ,解出AB,建立空间直角坐标系D-xyz,求出平面ABD的法向量,平面AED的法向量,即可得二面角B-AD-E的正弦值
,解出AB,建立空间直角坐标系D-xyz,求出平面ABD的法向量,平面AED的法向量,即可得二面角B-AD-E的正弦值
(1)证明:因为直角梯形ABCD中,AD∥BC,AB⊥BC,
所以AB⊥AD,
因为AB⊥AC,![]() ,所以AB⊥平面ADC,
,所以AB⊥平面ADC,
所以AB⊥CD,
因为BD⊥DC, ![]() ,
,
所以CD⊥平面ADB,
因为CD在平面BCD内,
所以平面ABD⊥平面BCD
(2)由(1)知AB⊥平面ADC,
所以二面角C-AB-D的平面角为∠CAD,
因为CD⊥平面ADB,所以AD⊥CD,
所以![]() ,得
,得![]() ,所以
,所以![]() ,
,
设![]() ,则
,则![]() ,
,
由题意可知![]()
![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() ,
,
如图所示,建立空间直角坐标系D-xyz,则
![]() ,
,
所以![]() ,
,
因为CD⊥平面ADB,所以令平面ADB的法向量为![]() ,
,
设平面AED的法向量为![]() ,则
,则
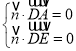 ,即
,即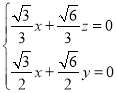 ,
,
取![]() ,则
,则![]() ,
,
设二面角B-AD-E的平面角为![]() ,
,
则![]() ,
,
所以![]() ,
,
所以二面角B-AD-E的正弦值为![]() ,
,

【题目】垃圾分类是对垃圾进行有效处置的一种科学管理方法.太原市为推进这项工作的实施,开展了“垃圾分类进小区”的评比活动.现有甲、乙两个小区采取不同的宣传与倡导方式对各自小区居民进行了有关垃圾分类知识的培训,并参加了评比活动,评委会随机从两个小区各选出20户家庭进行评比打分,每户成绩满分为100分,评分后得到如下茎叶图.
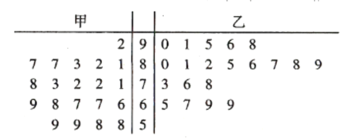
(1)依茎叶图判断哪个小区的平均分高?
(2)现从甲小区不低于80分的家庭中随机抽取两户,求分数为87的家庭至少有一户被抽中的概率;
(3)如果规定分数不低于85分的家庭为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为得分是否优秀与小区宣传培训方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为得分是否优秀与小区宣传培训方式有关?”
甲 | 乙 | 合计 | |
优秀 |
|
| |
不优秀 |
|
| |
合计 |
参考公式和数据: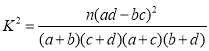 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】2019年1月1日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房货款利息、住房租金、赡养老人.某单位有老年员工140人,中年员工180人,青年员工80人,现采用分层抽样的方法,从该单位员工中抽取20人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如下:
员工\人数\专项 | 子女教育 | 继续教育 | 大病医疗 | 住房贷款利息 | 住房租金 | 赡养老人 |
老员工 | 4 | 0 | 2 | 2 | 0 | 3 |
中年员工 | 8 | 2 | 1 | 5 | 1 | 8 |
青年员工 | 1 | 2 | 0 | 1 | 2 | 1 |
(Ⅰ)在抽取的20人中,老年员工、中年员工、青年员工各有多少人;
(Ⅱ)从上表享受住房货款利息专项扣除的员工中随机选取2人,求选取2人都是中年员工的概率.