Question

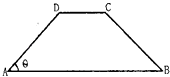
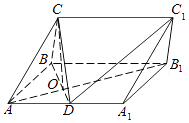
【题目】如图，在直四棱柱中，底面是梯形， .

(Ⅰ)求证： ；

(Ⅱ)若,点为线段的中点．请在线段上找一点,使平面，并说明理由.

Answer 1

【答案】(I)见解析(II) 线段的中点即为所求的点

【解析】试题分析：（1）证明线线垂直，可先证明线面垂直平面平面，故；（2）线段的中点即为所求的点，根据平行四边形，得到线线平行，进而得到线面平行。

解析：

(I)在直四棱柱中，

∵平面平面，

∴,

又∵,

∴平面.

∵平面，∴.

(II)线段的中点即为所求的点 [或：过作（或者）平行线交于点].

理由如下：取线段的中点，连结.

∵, ∴,

又∵, ∴.

又∵在梯形中， ,

∴四边形是平行四边形．

∴,

又∵,

∴

∵延长必过,∴四点共面，

∴不在平面内，即平面,

又∵平面，

∴平面.