题目内容
对“a,b,c是不全相等的正数”,给出如下判断:
①(a-b)2+(b-c)2+(c-a)2≠0;②a>b与a<b及a=b中至少有一个成立;
③a≠c,b≠c,a≠b不能同时成立,其中判断正确的个数是( )
①(a-b)2+(b-c)2+(c-a)2≠0;②a>b与a<b及a=b中至少有一个成立;
③a≠c,b≠c,a≠b不能同时成立,其中判断正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
选C
对于①:若a=b=c,则(a-b)2+(b-c)2+(c-a)2=0所以因为a,b,c是不全相等的正数, 所以(a-b)2+(b-c)2+(c-a)2≠0①正确;对于②:由于a>b与a<b及a=b三种情况均有可能所以②正确;对于③:由于a,b,c是不全相等的正数,因而可能是a≠c,b≠c,a≠b不同时成立或都者a≠c,b≠c,a≠b同时成立两种情况所以③错

练习册系列答案
相关题目
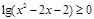 ;命题q:
;命题q: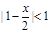 .若p是真命题,且q是假命题,求实数x的取值范围.
.若p是真命题,且q是假命题,求实数x的取值范围.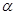 //平面
//平面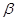 ,
,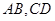 是夹在
是夹在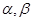 间的线段,若
间的线段,若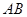 //
//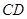 ,则
,则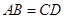 ;
;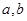 是异面直线,
是异面直线,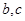 是异面直线,则
是异面直线,则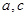 一定是异面直线;
一定是异面直线;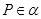 ,
,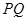 //
//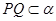 ;
;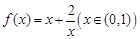 的最小值是
的最小值是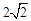 ;②对于任意实数
;②对于任意实数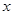 ,有
,有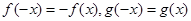 且
且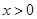 时,
时,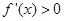 ,
, 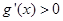 ,则
,则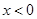 时,
时,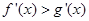 ;③如果
;③如果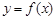 是可导函数,则
是可导函数,则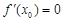 是函数
是函数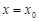 处取到极值的必要不充分条件;④已知存在实数
处取到极值的必要不充分条件;④已知存在实数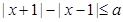 成立,则实数
成立,则实数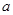 的取值范围是
的取值范围是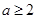 。其中正确的命题是___________.
。其中正确的命题是___________.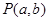 与点
与点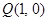 在直线
在直线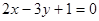 的两侧,则下列说法: ①
的两侧,则下列说法: ① 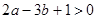 ; ②
; ② 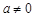 时,
时,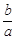 有最小值,无最大值;
有最小值,无最大值;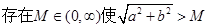 恒成立;
恒成立;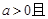
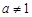 ,
,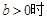 , 则
, 则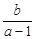 的取值范围为(-
的取值范围为(-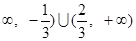 ;
;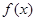 ,若存在区间
,若存在区间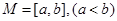 ,使得
,使得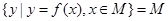 ,则称区间
,则称区间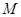 为函数
为函数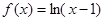 ②
②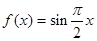 ③
③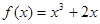 ④
④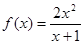 .
.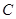 上的点的坐标都是方程
上的点的坐标都是方程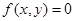 的解”是正确的,则下列命题中正确的是( )
的解”是正确的,则下列命题中正确的是( )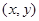 不在曲线
不在曲线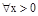 ,都有x>lnx”的否定;
,都有x>lnx”的否定;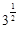 是有理数,则x是无理数”的逆否命题
是有理数,则x是无理数”的逆否命题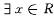 ,使得
,使得