题目内容
已知函数 ,若
,若 在区间
在区间 上单调递减,则
上单调递减,则 的取值范围是C
的取值范围是C
 ,若
,若 在区间
在区间 上单调递减,则
上单调递减,则 的取值范围是C
的取值范围是CA.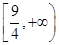 | B. | C. | D. |
B
试题分析:根据题意,由于函数
 ,若
,若 在区间
在区间 上单调递减,则说明导数
上单调递减,则说明导数 在
在 上恒成立,则根据不等式恒成立,结合二次方程根的分布问题可知,
上恒成立,则根据不等式恒成立,结合二次方程根的分布问题可知, ,那么可知
,那么可知 表示的 为区域内的点到原点距离平方的取值范围,那么结合线性区域可知,过点(0,
表示的 为区域内的点到原点距离平方的取值范围,那么结合线性区域可知,过点(0, )时,距离最大,则距离的平方为
)时,距离最大,则距离的平方为 ,因此答案为B
,因此答案为B点评:解决函数在区间上的单调性已知求参数的范围的问题,递增时令导函数大于等于0恒成立;递减时,令导数小于等于0恒成立.

练习册系列答案
相关题目
 轴上一点A分别向函数
轴上一点A分别向函数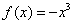 与函数
与函数 引不是水平方向的切线
引不是水平方向的切线 和
和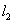 ,两切线
,两切线 轴相交于点B和点C,O为坐标原点,记△OAB的面积为
轴相交于点B和点C,O为坐标原点,记△OAB的面积为 ,△OAC的面积为
,△OAC的面积为 ,则
,则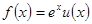 ,
,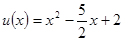 ,求函数
,求函数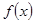 的极小值,
的极小值,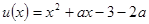 ,设
,设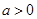 ,函数
,函数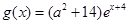 .若存在
.若存在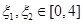 使得
使得 成立,求
成立,求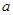 的取值范围.
的取值范围.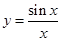 上的点
上的点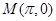 的切线方程为________________。
的切线方程为________________。 ,并设:
,并设: 
 ,
, 至少有3个实根;
至少有3个实根; 当
当 时,方程
时,方程 当
当 时,方程
时,方程




 元(
元( 万件.
万件. (万元)与每件产品的售价
(万元)与每件产品的售价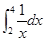 等于( )
等于( ) 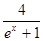 在点(0,2)处的切线方程为_______.
在点(0,2)处的切线方程为_______.