题目内容
16.已知f2(x+1)+f2(x)=9,求函数f(x)的周期.分析 令x取x-1代入f2(x+1)+f2(x)=9得:f2(x)+f2(x-1)=9,联立两个式子后化简,利用函数的周期定义分别求出函数的周期.
解答 解:∵f2(x+1)+f2(x)=9,
∴令x取x-1代入上式得,f2(x)+f2(x-1)=9,
则f2(x+1)+f2(x)=f2(x)+f2(x-1),
即f2(x+1)=f2(x-1),
∴[f(x+1)-f(x-1)][f(x+1)+f(x-1)]=0,
①、当f(x+1)-f(x-1)=0时,有f(x+1)=f(x-1),则f(x)=f(x+2),
∴函数f(x)的周期是2;
②当f(x+1)+f(x-1)=0时,有f(x+1)=-f(x-1),
则f(x+2)=-f(x),即f(x+4)=-f(x+2)=f(x),
∴函数f(x)的周期是4.
点评 本题考查函数的周期定义,以及化简、变形能力,属于中档题.

练习册系列答案
相关题目
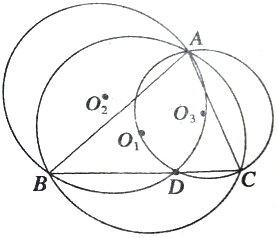 如图,D是△ABC的BC边上的一点,O1,O2和O3分别为△ABC,△ADB和△ADC外接圆的圆心,求证:A,O2,O1,O3四点共圆.
如图,D是△ABC的BC边上的一点,O1,O2和O3分别为△ABC,△ADB和△ADC外接圆的圆心,求证:A,O2,O1,O3四点共圆.