题目内容
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.

(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)图象见解析.
;(Ⅱ)图象见解析.
【解析】
(Ⅰ) 由函数![]() 的最大值为
的最大值为![]() ,可求得
,可求得![]() 的值,由图象相邻两条对称轴之间的距离为
的值,由图象相邻两条对称轴之间的距离为![]() 可求得周期,从而确定
可求得周期,从而确定![]() 的值,然后利用正弦函数的单调性解不式可得单调减区间,
的值,然后利用正弦函数的单调性解不式可得单调减区间,![]() 取特殊值即可得结果;(Ⅱ)利用函数图象的平移变换法则,可得到
取特殊值即可得结果;(Ⅱ)利用函数图象的平移变换法则,可得到![]() 的解析式,列表、描点、作图即可得结果.
的解析式,列表、描点、作图即可得结果.
(Ⅰ)∵函数f(x)的最大值是3,
∴A+1=3,即A=2.
∵函数图象的相邻两条对称轴之间的距离为![]() ,
,
∴最小正周期T=π,
∴ω=2.所以f(x)=2sin(2x-![]() )+1
)+1
令![]() +2kπ≤2x
+2kπ≤2x![]() ≤
≤![]() +2kπ,kZ,
+2kπ,kZ,
即![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,kZ,∵x[0,π],
+kπ,kZ,∵x[0,π],
∴f(x)的单调减区间为[![]() ,
,![]() ].
].
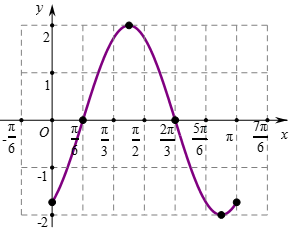
(Ⅱ)依题意得g(x)=f(x-![]() )-1=2sin(2x-
)-1=2sin(2x-![]() ),
),
列表得:

描点![]()
连线得g(x)在[0,π]内的大致图象.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目