题目内容
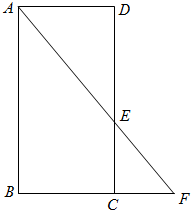 矩形ABCD中,AB=2,BC=1,E为CD上一点,且DE=x,延长AE交BC延长线于点F,设△CEF,△ADE的面积分别为S1,S2令S=S1+S2.
矩形ABCD中,AB=2,BC=1,E为CD上一点,且DE=x,延长AE交BC延长线于点F,设△CEF,△ADE的面积分别为S1,S2令S=S1+S2.(Ⅰ)求S关于x的解析式;
(Ⅱ)求S的最小值.
分析:(Ⅰ)由题意知△ADE∽△FCE,根据对应边成比例以及 AB=2,BC=1,DE=x,求得CE、CF的值,可得S=S1+S2=
×
×(2-x)+
×1×x.
(Ⅱ)由(Ⅰ)得S=x+
-2,利用基本不等式求得S的最小值.
| 1 |
| 2 |
| 2-x |
| x |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)得S=x+
| 2 |
| x |
解答:解:(Ⅰ)由题意知△ADE∽△FCE,∴
=
,又∵AB=2,BC=1,DE=x,
∴CE=2-x,CF=
.…(4分)
∴S=S1+S2=
×
×(2-x)+
×1×x=x+
-2(0<x<2).…(8分)
(Ⅱ)由(Ⅰ)得S=x+
-2≥2
-2=2
-2,当x=
时,即x=
时取等号,
所以S的最小值为2
-2.…(16分)
| DE |
| DA |
| CE |
| CF |
∴CE=2-x,CF=
| 2-x |
| x |
∴S=S1+S2=
| 1 |
| 2 |
| 2-x |
| x |
| 1 |
| 2 |
| 2 |
| x |
(Ⅱ)由(Ⅰ)得S=x+
| 2 |
| x |
x•
|
| 2 |
| 2 |
| x |
| 2 |
所以S的最小值为2
| 2 |
点评:本题主要考查求函数的解析式,基本不等式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知矩形ABCD中,AB=6,BC=6
已知矩形ABCD中,AB=6,BC=6 如图,在矩形ABCD中,
如图,在矩形ABCD中,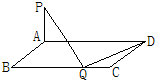 如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于
如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于