题目内容
在矩形ABCD中,AB=2,AD=3,如果向该矩形内随机投一点P,那么使得△ABP与△CDP的面积都不小于1的概率为
.
| 1 |
| 3 |
| 1 |
| 3 |
分析:根据题意,可得满足条件的P点位于矩形ABCD中间,长为2宽为1的一个小矩形当中,如图所示.由此结合几何概型计算公式,即可算出使△ABP与△CDP的面积都不小于1的概率.
解答: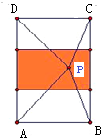 解:由题意,以AB为底边,要使△ABP面积不小于1,
解:由题意,以AB为底边,要使△ABP面积不小于1,
而S△ABP=
AB×h=h,即△ABP的高h≥1,
同理△CD的高h'≥1,
因此,P点到AB和CD的距离都要不小于1,相应的区域为图中阴影部分,
它的面积为S'=1×2=2
而矩形ABCD的面积为S=2×3=6
∴所求概率P=
=
故答案为:
 解:由题意,以AB为底边,要使△ABP面积不小于1,
解:由题意,以AB为底边,要使△ABP面积不小于1,而S△ABP=
| 1 |
| 2 |
同理△CD的高h'≥1,
因此,P点到AB和CD的距离都要不小于1,相应的区域为图中阴影部分,
它的面积为S'=1×2=2
而矩形ABCD的面积为S=2×3=6
∴所求概率P=
| S′ |
| S |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题给出几何概型,在矩形ABCD中求使得△ABP与△CDP的面积都不小于1的概率.着重考查了矩形、三角形的面积公式和几何概型计算公式等知识,属于基础题.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AD=2,AB=a(a>2),E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积.
如图,在矩形ABCD中,已知AD=2,AB=a(a>2),E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积.