题目内容
已知矩形ABCD中，AB=6，BC=6| 2 |
（1）求证：FD∥平面ABE；
（2）求二面角E-AB-C的余弦值．
分析：（1）由题意可取AB中点为M，连接MF，ME，证明DF∥ME，再由线面平行的判定定理证明FD∥平面ABE即可；
（2）在矩形ABCD中，连接AC交BE于G，在图二中作G′H⊥AB于H，连CH，可先由向量与垂直的对应关系在平面矩形中先证明BE与AC垂直，由于翻折不改变此垂直关系，结合面面垂直与三垂线定理证明出角GHC是二面角E-AB-C的平面角，然后在相应的三角形中求出其余弦值的大小即可得到所求的二面角．
（2）在矩形ABCD中，连接AC交BE于G，在图二中作G′H⊥AB于H，连CH，可先由向量与垂直的对应关系在平面矩形中先证明BE与AC垂直，由于翻折不改变此垂直关系，结合面面垂直与三垂线定理证明出角GHC是二面角E-AB-C的平面角，然后在相应的三角形中求出其余弦值的大小即可得到所求的二面角．
解答：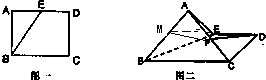
解：（1）由题意，如图，可取AB中点为M，连接MF，ME，由于E为AD的中点F为AC的中点
∴MF
BC
DE
∴四边形MFDE是平行四边形
∴DF∥ME，又MF?平面ABE，FD?平面ABE
∴FD∥平面ABE
（2）在矩形ABCD中，连接AC交BE于G，则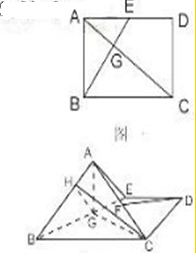
•
=(
+
)•(
+
)=-
2+
•
=-36+36=0
∴
⊥
，又AB=6，BC=6
∴AC=6
，BE=3
∴AG=2
，GC=4
在图二中作G′H⊥AB于H，连CH，
∵CG⊥BE，所以平面ABE⊥平面BCDE，
∴CG⊥平面ABE，
∵GH⊥AB，由三垂线定理知GH⊥AB，
∴∠GHC是二面角E-AB-C的平面角，
∵GH×AB=AG×BG，GB=2
∴GH=
=
=2
，
∵tan∠CHG=
=
=
∴cos∠CHG=
即二面角E-AB-C的余弦值为
解：（1）由题意，如图，可取AB中点为M，连接MF，ME，由于E为AD的中点F为AC的中点∴MF
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴四边形MFDE是平行四边形
∴DF∥ME，又MF?平面ABE，FD?平面ABE
∴FD∥平面ABE
（2）在矩形ABCD中，连接AC交BE于G，则
| BE |
| AC |
| BA |
| AE |
| AB |
| BC |
| AB |
| AE |
| BC |
∴
| BE |
| AC |
| 2 |
∴AC=6
| 3 |
| 6 |
∴AG=2
| 3 |
| 3 |
∵CG⊥BE，所以平面ABE⊥平面BCDE，
∴CG⊥平面ABE，
∵GH⊥AB，由三垂线定理知GH⊥AB，
∴∠GHC是二面角E-AB-C的平面角，
∵GH×AB=AG×BG，GB=2
| 6 |
∴GH=
| AG×BG |
| AB |
2
| ||||
| 6 |
| 2 |
∵tan∠CHG=
| CG |
| GH |
4
| ||
2
|
| 6 |
∴cos∠CHG=
| ||
| 7 |
即二面角E-AB-C的余弦值为
| ||
| 7 |
点评：本题考查了二面角的求法，线面平行的证明，是立体几何中常考的题型，解题的关键是熟练掌握二面角平面角的作法与线面平行的判定定理，本题考查了数形结合的思想与推理证明的能力，是高考中常考的题型，难度较大，熟练掌握相关方法与技巧是解题的关键
练习册系列答案
相关题目
已知矩形ABCD中，AB=2AD=4，E为CD的中点，沿AE将△AED折起，使DB=2
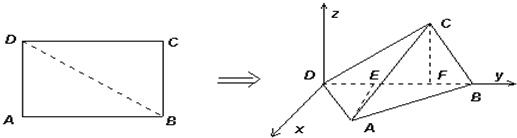
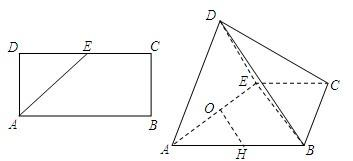
（2013•临沂二模）如图，已知矩形ABCD中，AB=2AD=2，O为CD的中点，沿AO将三角形AOD折起，使