题目内容
在平面直角坐标系 中,直线
中,直线 与圆
与圆 相交于
相交于 两点,则弦
两点,则弦 的长等于( )
的长等于( )
A. | B. | C.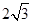 | D.1 |
C
解析试题分析:由直线与圆相交的性质可知, ,要求AB,只要求解圆心到直线3x+4y-5=0的距离.
,要求AB,只要求解圆心到直线3x+4y-5=0的距离.
由题意可得,圆心(0,0)到直线3x+4y-5=0的距离d=
则由圆的性质可得,(
即AB=2 ,故选C
,故选C
考点:本试题考查直线与圆位置关系。
点评:对于直线与圆的位置关系中相交的情况,利用圆的半径和圆心距和半弦长来结合勾股定理得到弦长是解决试题的关键,属于基础题。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知圆O: ,直线
,直线 过点
过点 ,且与直线OP垂直,则直线
,且与直线OP垂直,则直线 的方程为( )
的方程为( )
A. | B. | C. | D. |
若直线 截得的弦最短,则直线
截得的弦最短,则直线 的方程是
的方程是
A. | B. |
C. | D. |
过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是( )
| A.(x-3)2+(y+1)2=4 | B.(x-1)2+(y-1)2=4 |
| C.(x+3)2+(y-1)2=4 | D.(x+1)2+(y+1)2=4 |
圆 :
: 与圆
与圆 :
: 的位置关系是( )
的位置关系是( )
| A.相交 | B.外切 | C.内切 | D.相离 |
一束光线从点 出发经
出发经 轴反射,到达圆C:
轴反射,到达圆C: 上一点的最短路程是( )
上一点的最短路程是( )
| A.4 | B.5 |
C.3 -1 -1 | D.2 |
直线 相切,则实数
相切,则实数 等于( )
等于( )
A. | B. | C. | D. |
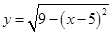 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )



 ,则直线倾斜角的取值范围是( )
,则直线倾斜角的取值范围是( )


