题目内容
已知函数y=f(x)在定义域(-
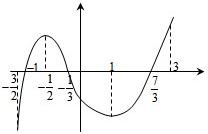
,3)上可导,y=f(x)的图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是______.
| 3 |
| 2 |

由f(x)的图象知x∈(-
,-
)时,递增,f′(x)>0;xf′(x)≤0?x≤0∴x∈(-
,-
)
x∈(-
,1)时,f(x)递减,f′(x)<0,∴xf′(x)≤0?x≥0∴x∈[0,1]
x∈(1,3)时,f(x)递增,f′(x)>0,∴xf′(x)≤0?x≤0无解
故答案为:[0,1]∪(-
,-
]
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
x∈(-
| 1 |
| 2 |
x∈(1,3)时,f(x)递增,f′(x)>0,∴xf′(x)≤0?x≤0无解
故答案为:[0,1]∪(-
| 3 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
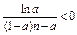 对于任意正整数n恒成立, 则实数a的取值范围是
对于任意正整数n恒成立, 则实数a的取值范围是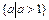
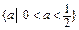
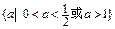
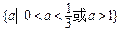
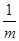 +
+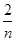 的最小值等于________.
的最小值等于________.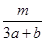 -
-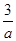 -
-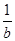 ≤0恒成立,则m的最大值为( )
≤0恒成立,则m的最大值为( )